Separation of variables
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص284-285
2025-11-22
13
Separation of variables
Some partial differential equations can be simplified by the separation of variables technique, which divides the equation into two or more ordinary differential equations, one for each variable. An important application of this procedure, as we shall see, is the separation of the Schrödinger equation for the hydrogen atom into equations that describe the radial and angular variation of the wavefunction. The technique is particularly simple for a two-dimensional square well, as can be seen by testing whether a solution of eqn 9.10 can be found by writing the wavefunction as a product of functions, one depending only on x and the other only on y:
ψ(x,y)=X(x)Y(y)
With this substitution, we show in the Justification below that eqn 9.10 separates into two ordinary differential equations, one for each coordinate:
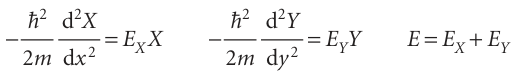
The quantity EX is the energy associated with the motion of the particle parallel to the x-axis, and likewise for EY and motion parallel to the y-axis.
Justification 9.3The separation of variables technique applied to the particle in a two-dimensional box The first step in the justification of the separability of the wavefunction into the product of two functions X and Y is to note that, because X is independent of y and Y is independent of x, we can write
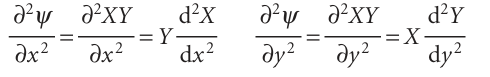
Then eqn 9.10 becomes
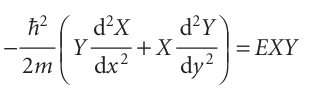
When both sides are divided by XY, we can rearrange the resulting equation into
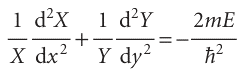
The first term on the left is independent of y, so if y is varied only the second term can change. But the sum of these two terms is a constant given by the right-hand side of the equation; therefore, even the second term cannot change when y is changed. In other words, the second term is a constant, which we write −2mEY/h2. By a similar argument, the first term is a constant when x changes, and we write it −2mEX/h2, and E=EX+EY. Therefore, we can write
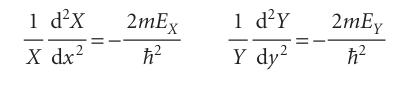
which rearrange into the two ordinary (that is, single variable) differential equations in eqn 9.11.
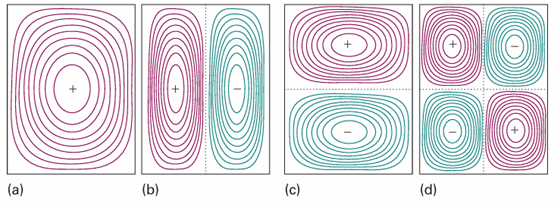
Fig. 9.7The wavefunctions for a particle confined to a rectangular surface depicted as contours of equal amplitude. (a) n1=1, n2=1, the state of lowest energy, (b) n1=1, n2=2, (c) n1=2, n2=1, and (d) n1=2, n2=2.
Each of the two ordinary differential equations in eqn 9.11 is the same as the one-dimensional square-well Schrödinger equation. We can therefore adapt the results in eqn 9.4 without further calculation:
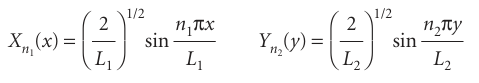
Then, because ψ=X Y and E=EX+EY, we obtain
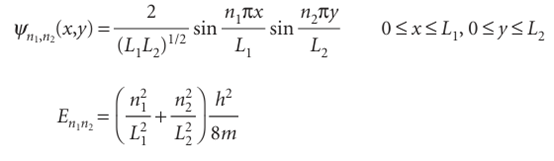
ently. Some of these functions are plotted in Fig. 9.7. They are the two-dimensional versions of the wavefunctions shown in Fig. 9.3. Note that two quantum numbers are needed in this two-dimensional problem. We treat a particle in a three-dimensional box in the same way. The wavefunctions have another factor (for the z-dependence), and the energy has an additional term in n32/L32. Solution of the Schrödinger equation by the separation of variables technique then gives
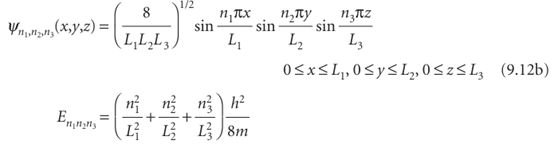
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
