The Stefan-Boltzmann Law
المؤلف:
LibreTexts Project
المصدر:
................
الجزء والصفحة:
.................
30-1-2020
3769
The Stefan-Boltzmann Law
The first quantitative conjecture based on experimental observations was the Stefan-Boltzmann Law (1879) which states the total power (i.e., integrated over all emitting frequencies in Figure 1.1) radiated from one square meter of black surface goes as the fourth power of the absolute temperature (Figure 1.3):
P=σT4(1.1.1)
where
- P is the total amount of radiation emitted by an object per square meter (Watts m−2)
- σis a constant called the Stefan-Boltzman constant (5.67×10−8 Watts m−2K−4
- T is the absolute temperature of the object (in K) at different temperatures.
The Stefan-Boltzmann Law is easily observed by comparing the integrated value (i.e., under the curves) of the experimental black-body radiation distribution in Figure 1.1
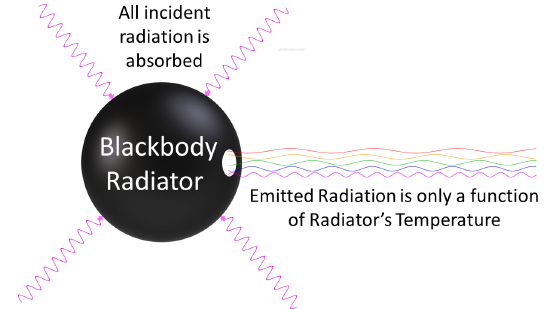
Figure 1.1.2:
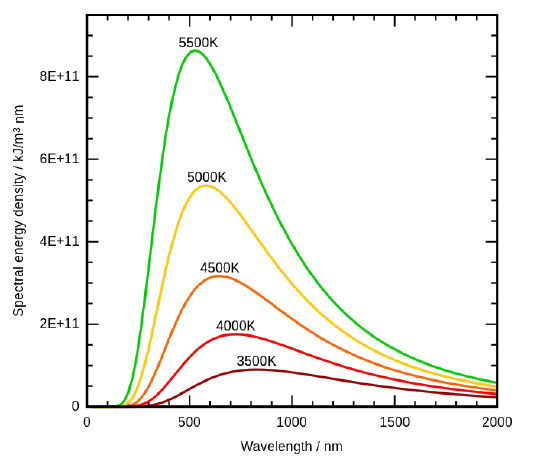
Figure 1.1:
In 1884, Boltzmann derived this T4 behavior from theory by applying classical thermodynamic reasoning to a box filled with electromagnetic radiation, using Maxwell’s equations to relate pressure to energy density. That is, the tiny amount of energy coming out of the hole (Figure 1.1.2 ) would of course have the same temperature dependence as the radiation intensity inside.
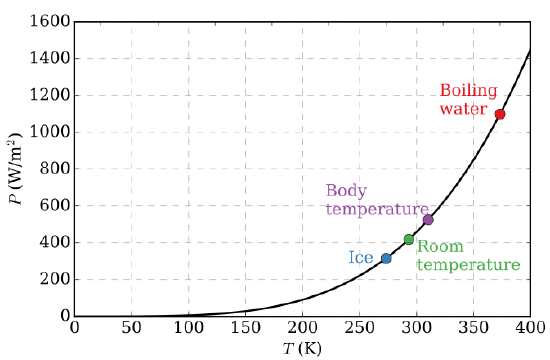
Figure 1.3 : Graph of a function of total emitted energy of a blackbody proportional to the fourth power of its thermodynamic temperature T according to the Stefan–Boltzmann law. (CC -SA-BY 4.0; Nicoguaro).
Example 1.1 The sun’s surface temperature is 5700 K.
- How much power is radiated by the sun?
- Given that the distance to earth is about 200 sun radii, what is the maximum power possible from a one square kilometer solar energy installation?
Solution
(a) First, we calculate the area of the sun followed by the flux (power). The sun has a radius of 6.96×108m
The area of the sun is A=4πR2
A=4(3.1416)(6.96×108m)2 = 6.08×1018m2 The power radiated from the sun (via Stefan-Boltzmann Law) is P=σT4.
P=(5.67×10−8Wattsm−2K−4)(5700K)4=5.98×107Watts/m2
This value is per square meter.
(b) To calculate the total power radiated by the sun is thus:
Ptotal=PA=(5.98×107Watts/m2)(6.08×1018m2)=3.6×1026Watts
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
