Quantization
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص 259-260
2025-11-20
61
Quantization
The Born interpretation puts severe restrictions on the acceptability of wave functions. The principal constraint is that ψ must not be infinite anywhere. If it were, the integral in eqn 8.17 would be infinite (in other words, ψ would not be square-integrable) and the normalization constant would be zero. The normalized function would then be zero everywhere, except where it is infinite, which would be unacceptable. The requirement that ψ is finite everywhere rules out many possible solutions of the Schrödinger equation, because many mathematically acceptable solutions rise to infinity and are therefore physically unacceptable. We shall meet several examples shortly. The requirement that ψ is finite everywhere is not the only restriction implied by the Born interpretation. We could imagine (and in Section 9.6a will meet) a solution of the Schrödinger equation that gives rise to more than one value of |ψ|2at a single point. The Born interpretation implies that such solutions are unacceptable, because it would be absurd to have more than one probability that a particle is at the same point. This restriction is expressed by saying that the wavefunction must be single-valued; that is, have only one value at each point of space.
The Schrödinger equation itself also implies some mathematical restrictions on the type of functions that will occur. Because it is a second-order differential equation, the second derivative of ψ must be well-defined if the equation is to be applicable everywhere. We can take the second derivative of a function only if it is continuous (so there are no sharp steps in it, Fig. 8.24) and if its first derivative, its slope, is continuous (so there are no kinks). At this stage we see that ψ must be continuous, have a continuous slope, be single-valued, and be square-integrable. An acceptable wavefunction cannot be zero everywhere, because the particle it describes must be somewhere. These are such severe restrictions that acceptable solutions of the Schrödinger equation do not in general exist for arbitrary values of the energy E. In other words, a particle may possess only certain energies, for otherwise its wavefunction would be physically unacceptable. That is, the energy of a particle is quantized. We can find the acceptable energies by solving the Schrödinger equation for motion of various kinds, and selecting the solutions that conform to the restrictions listed above. That is the task of the next chapter.
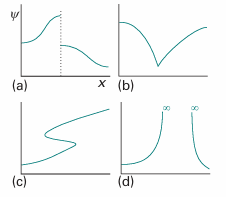
Fig. 8.24 The wavefunction must satisfy stringent conditions for it to be acceptable. (a) Unacceptable because it is not continuous; (b) unacceptable because its slope is discontinuous; (c) unacceptable because it is not single-valued; (d) unacceptable because it is infinite over a finite region.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
