The properties of the solutions
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص280-282
2025-11-22
15
The properties of the solutions
Figure 9.3 shows some of the wavefunctions of a particle in a box: they are all sine functions with the same amplitude but different wavelengths. Shortening the wave length results in a sharper average curvature of the wavefunction and therefore an increase in the kinetic energy of the particle. Note that the number of nodes (points where the wavefunction passes through zero) also increases as nincreases, and that the wavefunctionψnhasn−1 nodes. Increasing the number of nodes between walls of a given separation increases the average curvature of the wavefunction and hence the kinetic energy of the particle. The linear momentum of a particle in a box is not well defined because the wave function sin kxis a standing wave and, like the example of cos kxtreated in Section 8.5d, not an eigenfunction of the linear momentum operator. However, each wave function is a superposition of momentum eigenfunctions:
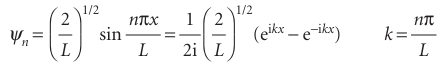
It follows that measurement of the linear momentum will give the value +kh for half the measurements of momentum and −kh for the other half. This detection of oppos ite directions of travel with equal probability is the quantum mechanical version of the classical picture that a particle in a box rattles from wall to wall, and in any given period spends half its time travelling to the left and half travelling to the right.
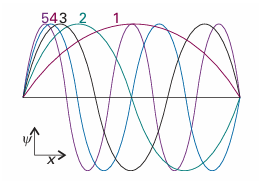
Fig. 9.3The first five normalized wavefunctions of a particle in a box. Each wavefunction is a standing wave, and successive functions possess one more half wave and a correspondingly shorter wavelength.
Because n cannot be zero, the lowest energy that the particle may possess is not zero (as would be allowed by classical mechanics, corresponding to a stationary particle) but
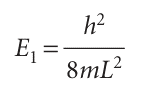
This lowest, irremovable energy is called the zero-point energy. The physical origin of the zero-point energy can be explained in two ways. First, the uncertainty principle requires a particle to possess kinetic energy if it is confined to a finite region: the location of the particle is not completely indefinite, so its momentum cannot be precisely zero. Hence it has nonzero kinetic energy. Second, if the wavefunction is to be zero at the walls, but smooth, continuous, and not zero everywhere, then it must be curved, and curvature in a wavefunction implies the possession of kinetic energy. The separation between adjacent energy levels with quantum numbers n and n + 1 is
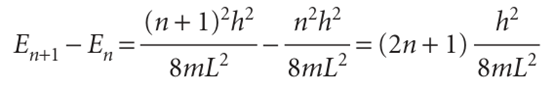
This separation decreases as the length of the container increases, and is very small when the container has macroscopic dimensions. The separation of adjacent levels becomes zero when the walls are infinitely far apart. Atoms and molecules free to move in normal laboratory-sized vessels may therefore be treated as though their translational energy is not quantized. The translational energy of completely free particles (those not confined by walls) is not quantized.
The probability density for a particle in a box is
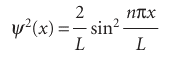
and varies with position. The nonuniformity is pronounced when n is small (Fig. 9.4), but—provided we ignore the increasingly rapid oscillations—ψ2(x) becomes more uniform as n increases. The distribution at high quantum numbers reflects the classical result that a particle bouncing between the walls spends, on the average, equal times at all points. That the quantum result corresponds to the classical prediction at high quantum numbers is an illustration of the correspondence principle, which states that classical mechanics emerges from quantum mechanics as high quantum numbers are reached.
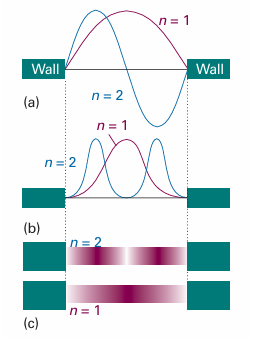
Fig. 9.4 (a) The first two wavefunctions, (b) the corresponding probability distributions, and (c) a representation of the probability distribution in terms of the darkness of shading.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
