Superpositions and expectation values
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص266-269
2025-11-22
21
Superpositions and expectation values
Suppose now that the wavefunction is the one given in eqn 8.19 (with A = B). What is the linear momentum of the particle it describes? We quickly run into trouble if we use the operator technique. When we operate with px, we find
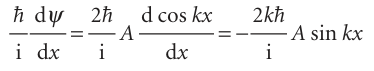
This expression is not an eigenvalue equation, because the function on the right (sin kx) is different from that on the left (cos kx).
When the wavefunction of a particle is not an eigenfunction of an operator, the property to which the operator corresponds does not have a definite value. However, in the current example the momentum is not completely indefinite because the cosine wavefunction is a linear combination, or sum, of eikx and e−ikx, and these two functions, as we have seen, individually correspond to definite momentum states. We say that the total wavefunction is a superposition of more than one wavefunction. Symbolically we can write the superposition as
The interpretation of this composite wavefunction is that, if the momentum of the particle is repeatedly measured in a long series of observations, then its magnitude will found to be k$ in all the measurements (because that is the value for each com ponent of the wavefunction). However, because the two component wavefunctions occur equally in the superposition, half the measurements will show that the particle is moving to the right (px =+k$), and half the measurements will show that it is moving to the left (px =−k$). According to quantum mechanics, we cannot predict in which direction the particle will in fact be found to be travelling; all we can say is that, in a long series of observations, if the particle is described by this wavefunction, then there are equal probabilities of finding the particle travelling to the right and to the left. The same interpretation applies to any wavefunction written as a linear com bination of eigenfunctions of an operator. Thus, suppose the wavefunction is known to be a superposition of many different linear momentum eigenfunctions and written as the linear combination
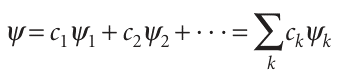
where the ck are numerical (possibly complex) coefficients and the ψk correspond to different momentum states. The functions ψk are said to form a complete set in the sense that any arbitrary function can be expressed as a linear combination of them. Then according to quantum mechanics:
1 When the momentum is measured, in a single observation one of the eigenvalues corresponding to the ψk that contribute to the superposition will be found.
2 The probability of measuring a particular eigenvalue in a series of observations is proportional to the square modulus (|ck|2) of the corresponding coefficient in the linear combination.
3 The average value of a large number of observations is given by the expectation value, Ω, of the operator Ω corresponding to the observable of interest.
The expectation value of an operator Ω is defined as
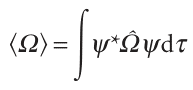
This formula is valid only for normalized wavefunctions. As we see in the Justification below, an expectation value is the weighted average of a large number of observations of a property.
Justification 8.4The expectation value of an operator If ψ is an eigenfunction of Ω with eigenvalue ω, the expectation value of Ω is
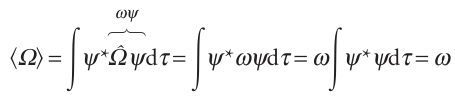
Because ω is a constant and may be taken outside the integral, and the resulting integral is equal to 1 for a normalized wavefunction. The interpretation of this expression is that, because every observation of the property Ω results in the value ω (because the wavefunction is an eigenfunction of Ω) , the mean value of all the observations is also ω.
A wavefunction that is not an eigenfunction of the operator of interest can be written as a linear combination of eigenfunctions. For simplicity, suppose the wave function is the sum of two eigenfunctions (the general case, eqn 8.33, can easily be developed).
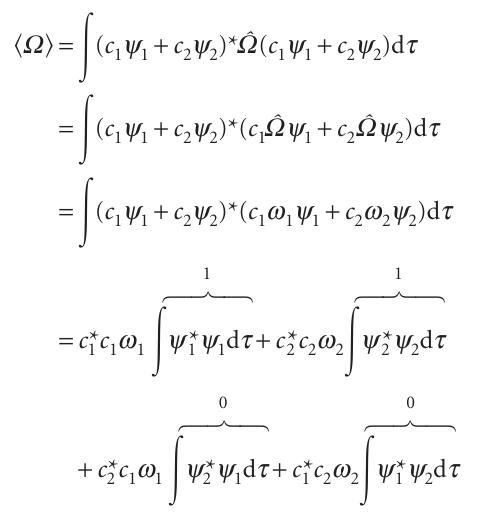
The first two integrals on the right are both equal to 1 because the wavefunctions are individually normalized. Because ψ1 and ψ2 correspond to different eigenvalues of an hermitian operator, they are orthogonal, so the third and fourth integrals on the right are zero. We can conclude that
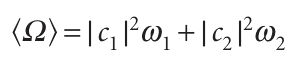
This expression shows that the expectation value is the sum of the two eigenvalues weighted by the probabilities that each one will be found in a series of measurements. Hence, the expectation value is the weighted mean of a series of observations.
The mean kinetic energy of a particle in one dimension is the expectation value of the operator given in eqn 8.28. Therefore, we can write
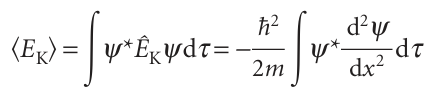
This conclusion confirms the previous assertion that the kinetic energy is a kind of average over the curvature of the wavefunction: we get a large contribution to the observed value from regions where the wavefunction is sharply curved (so d2ψ/dx2 is large) and the wavefunction itself is large (so that ψ* is large too)
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
