The Born interpretation of the wavefunction
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص256-257
2025-11-20
52
The Born interpretation of the wavefunction
A principal tenet of quantum mechanics is that the wavefunction contains all the dynamical information about the system it describes. Here we concentrate on the information it carries about the location of the particle. The interpretation of the wavefunction in terms of the location of the particle is based on a suggestion made by Max Born. He made use of an analogy with the wave theory of light, in which the square of the amplitude of an electromagnetic wave in a region is interpreted as its intensity and therefore (in quantum terms) as a measure of the probability of finding a photon present in the region. The Born interpretation of the wavefunction focuses on the square of the wavefunction (or the square modulus, |ψ|2 = ψ*ψ, if ψ is complex). It states that the value of |ψ|2 at a point is proportional to the probability of finding the particle in a region around that point. Specifically, for a one-dimensional system (Fig. 8.19): If the wavefunction of a particle has the value ψ at some point x, then the prob ability of finding the particle between x and x + dx is proportional to |ψ|2dx. Thus, |ψ|2 is the probability density, and to obtain the probability it must be multi plied by the length of the infinitesimal region dx. The wavefunction ψ itself is called the probability amplitude. For a particle free to move in three dimensions (for example, an electron near a nucleus in an atom), the wavefunction depends on the point dr with coordinates x, y, and z, and the interpretation of ψ(r) is as follows (Fig. 8.20): If the wavefunction of a particle has the value ψ at some point r, then the prob ability of finding the particle in an infinitesimal volume dτ = dxdydz at that point is proportional to |ψ2 dτ. The Born interpretation does away with any worry about the significance of a negative (and, in general, complex) value of ψ because |ψ|2 is real and never negative. There is no direct significance in the negative (or complex) value of a wavefunction: only the square modulus, a positive quantity, is directly physically significant, and both negative and positive regions of a wavefunction may correspond to a high probability of finding a particle in a region (Fig. 8.21). However, later we shall see that the presence of positive and negative regions of a wavefunction is of great indirect significance, because it gives rise to the possibility of constructive and destructive interference between different wavefunctions.
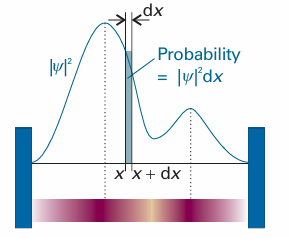
Fig. 8.19 The wavefunction ψ is a probability amplitude in the sense that its square modulus (ψ*ψ or |ψ|2) is a probability density. The probability of finding a particle in the region dx located at x is proportional to |ψ|2dx. We represent the probability density by the density of shading in the superimposed band.
Fig. 8.20The Born interpretation of the wavefunction in three-dimensional space implies that the probability of finding the particle in the volume element dτ=dxdydz at some location ris proportional to the product of dτ and the value of |ψ|2at that location.
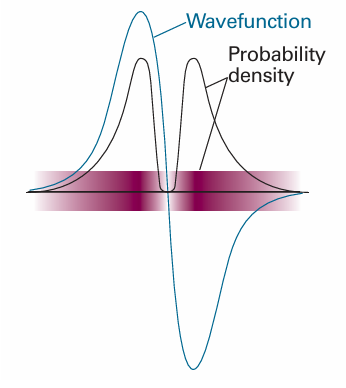
Fig. 8.21The sign of a wavefunction has no direct physical significance: the positive and negative regions of this wavefunction both correspond to the same probability distribution (as given by the square modulus of ψ and depicted by the density of shading).
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
