Heat capacities
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص247-249
2025-11-20
58
Heat capacities
In the early nineteenth century, the French scientists Pierre-Louis Dulong and Alexis Thérèse Petit determined the heat capacities of a number of monatomic solids. On the basis of some somewhat slender experimental evidence, they proposed that the molar heat capacities of all monatomic solids are the same and (in modern units) close to 25 J K−1 mol−1. Dulong and Petit’s law is easy to justify in terms of classical physics. If classical physics were valid, the equipartition principle could be used to calculate the heat capacity of a solid. According to this principle, the mean energy of an atom as it oscillates about its mean position in a solid is kT for each direction of displacement. As each atom can oscillate in three dimensions, the average energy of each atom is 3kT; for N atoms the total energy is 3NkT. The contribution of this motion to the molar internal energy is therefore
Um=3NAkT=3RT
because NAk = R, the gas constant. The molar constant volume heat capacity (see Comment8.3) is then predicted to be
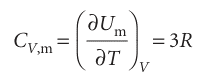
This result, with 3R = 24.9 J K−1 mol−1, is in striking accord with Dulong and Petit’s value.
Unfortunately (this time, for Dulong and Petit), significant deviations from their law were observed when advances in refrigeration techniques made it possible to measure heat capacities at low temperatures. It was found that the molar heat capacities of all monatomic solids are lower than 3R at low temperatures, and that the values approach zero as T → 0. To account for these observations, Einstein (in 1905) assumed that each atom oscillated about its equilibrium position with a single frequency ν. He then invoked Planck’s hypothesis to assert that the energy of oscillation is confined to discrete values, and specifically to nhν, where n is an integer. Einstein first calculated the contribution of the oscillations of the atoms to the total molar energy of the metal (by a method described in Section 16.4) and obtained
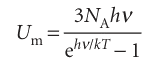
in place of the classical expression 3RT. Then he found the molar heat capacity by differentiating Um with respect to T. The resulting expression is now known as the Einstein formula:
The Einstein temperature, θE= hν/k, is a way of expressing the frequency of oscillation of the atoms as a temperature: a high frequency corresponds to a high Einstein temperature. At high temperatures (when T>>θE) the exponentials in f can be expanded as 1+θE/T+· · · and higher terms ignored (see Comment8.2). The result is
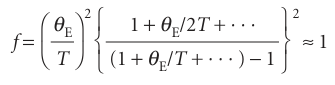
Consequently, the classical result (CV,m=3R) is obtained at high temperatures. At low temperatures, when T<<θE,
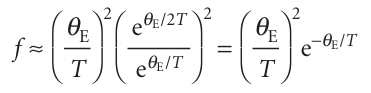
The strongly decaying exponential function goes to zero more rapidly than 1/T goes to infinity; so f→0 as T→0, and the heat capacity therefore approaches zero too. We see that Einstein’s formula accounts for the decrease of heat capacity at low temperatures. The physical reason for this success is that at low temperatures only a few oscillators possess enough energy to oscillate significantly. At higher temperatures, there is enough energy available for all the oscillators to become active: all 3N oscillators contribute, and the heat capacity approaches its classical value. Figure 8.8 shows the temperature dependence of the heat capacity predicted by the Einstein formula. The general shape of the curve is satisfactory, but the numerical agreement is in fact quite poor. The poor fit arises from Einstein’s assumption that all the atoms oscillate with the same frequency, whereas in fact they oscillate over a range of frequencies from zero up to a maximum value, νD. This complication is taken into account by averaging over all the frequencies present, the final result being the Debye formula:
Where θD=hνD/kis the Debye temperature (for a derivation, see Further reading). The integral in eqn 8.9 has to be evaluated numerically, but that is simple with mathematical software. The details of this modification, which, as Fig. 8.9 shows, gives improved agreement with experiment, need not distract us at this stage from the main conclusion, which is that quantization must be introduced in order to explain the thermal properties of solids.
Fig. 8.8 Experimental low-temperature molar heat capacities and the temperature dependence predicted on the basis of Einstein’s theory. His equation (eqn 8.7) accounts for the dependence fairly well, but is everywhere too low.
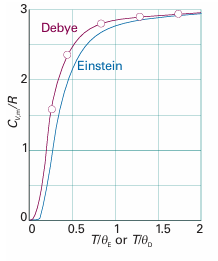
Fig. 8.9 Debye’s modification of Einstein’s calculation (eqn 8.9) gives very good agreement with experiment. For copper, T/θD =2 corresponds to about 170 K, so the detection of deviations from Dulong and Petit’s law had to await advances in low-temperature physics.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
