Normalization
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص257-259
2025-11-20
62
Normalization
A mathematical feature of the Schrödinger equation is that, if ψ is a solution, then so is Nψ, where Nis any constant. This feature is confirmed by noting that ψ occurs in every term in eqn 8.13, so any constant factor can be cancelled. This freedom to vary the wavefunction by a constant factor means that it is always possible to find a normalization constant, N, such that the proportionality of the Born interpretation becomes an equality.
We find the normalization constant by noting that, for a normalized wavefunction Nψ, the probability that a particle is in the region dx is equal to (Nψ*) (Nψ) dx (we are taking N to be real). Furthermore, the sum over all space of these individual probabilities must be 1 (the probability of the particle being somewhere is 1). Expressed mathematically, the latter requirement is
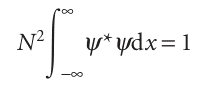
Almost all wavefunctions go to zero at sufficiently great distances so there is rarely any difficulty with the evaluation of this integral, and wavefunctions for which the integral in eqn 8.15 exists (in the sense of having a finite value) are said to be ‘square integrable’. It follows that
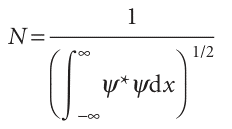
Therefore, by evaluating the integral, we can find the value of N and hence ‘normalize’ the wavefunction. From now on, unless we state otherwise, we always use wave functions that have been normalized to 1; that is, from now on we assume that ψ already includes a factor that ensures that (in one dimension)
In three dimensions, the wavefunction is normalized if
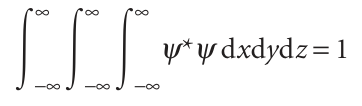
or, more succinctly, if
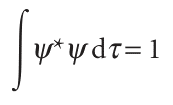
where dτ = dxdydz and the limits of this definite integral are not written explicitly: in all such integrals, the integration is over all the space accessible to the particle. For systems with spherical symmetry it is best to work in spherical polar coordinates r, θ, and φ(Fig. 8.22): x = r sin θ cos φ, y = r sin θ sin φ, z = r cos θ. The volume element in spherical polar coordinates is dτ = r2 sinθ dr dθ dφ. To cover all space, the radius r ranges from 0 to ∞, the colatitude, θ, ranges from 0 to π, and the azimuth, φ, ranges from 0 to 2π (Fig. 8.23), so the explicit form of eqn 6.17c is
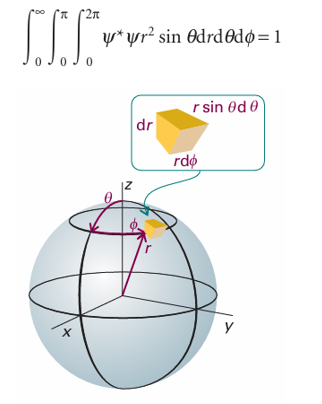
Fig. 8.22 The spherical polar coordinates used for discussing systems with spherical symmetry.
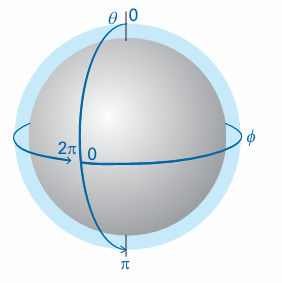
Fig. 8.23 The surface of a sphere is covered by allowing θ to range from 0 to π, and then sweeping that arc around a complete circle by allowing φ to range from 0 to 2π.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
