Octahedral complexes

Key points: In the presence of an octahedral crystal field, d orbitals are split into a lower-energy triply degenerate set (t_2g) and a higher-energy doubly degenerate set (e_g) separated by an energy Δ_O; the ligand-field splitting parameter increases along a spectrochemical series of ligands and varies with the identity and charge of the metal atom. In the model of an octahedral complex used in crystal-field theory, six-point negative charges representing the ligands are placed in an octahedral array around the central metal ion. These charges (which we shall refer to as the ‘ligands’) interact strongly with the

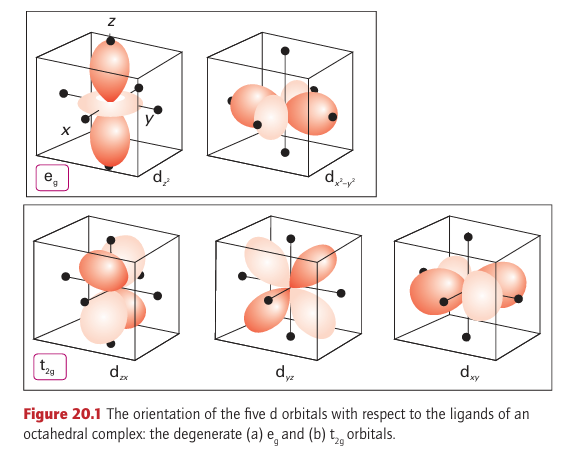
central metal ion, and the stability of the complex stems in large part from this attractive interaction between opposite charges. However, there is a much smaller but very important secondary effect arising from the fact that electrons in different d orbitals interact with the ligands to different extents. Although this differential interaction is little more than about 10 per cent of the overall metal ligand interaction energy, it has major consequences for the properties of the complex and is the principal focus of this section. Electrons in dz₂ and dx₂ y₂ orbitals (which are of symmetry type eg in O_h; Section 6.1) are concentrated close to the ligands, along the axes, whereas electrons in d_xy, d_yz, and dzx orbitals (which are of symmetry type t2g ) are concentrated in regions that lie between the ligands (Fig. 20.1). As a result, the former are repelled more strongly by the negative charge on the ligands than the latter and lie at a higher energy. Group theory shows that the two eg orbitals have the same energy (although this is not readily apparent from drawings), and that the three t₂g orbitals also have the same energy. This simple model leads to an energy-level diagram in which the three degenerate t2g orbitals lie below the two degenerate eg orbitals (Fig. 20.2). The separation of the two sets of orbitals is called the ligand-field splitting parameter, O (where the subscript O signifies an octahedral crystal field).

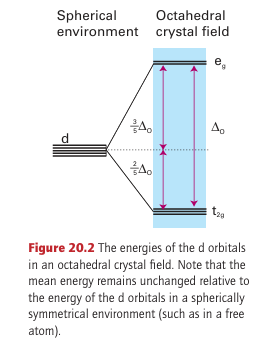
The energy level that corresponds to the hypothetical spherically symmetrical environ ment (in which the negative charge due to the ligands is evenly distributed over a sphere instead of being localized at six points) defines the barycentre of the array of levels, with the two eg orbitals lying at 3/5 ∆_O above the barycentre and the three t₂g orbitals lying at 2/5 ∆_O below it. As in the representation of the configurations of atoms, a superscript is used to indicate the number of electrons in each set, for example t₂g².

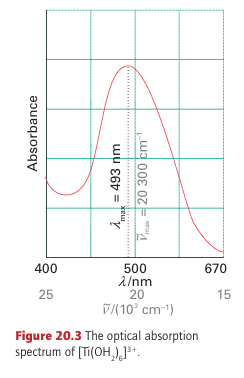
The simplest property that can be interpreted by crystal-field theory is the absorption spectrum of a one-electron complex. Figure 20.3 shows the optical absorption spectrum of the d1 hexaaquatitanium (III) ion, [Ti(OH₂)₆]³⁺. Crystal-field theory assigns the first absorption maximum at 493 nm (20300 cm^-1) to the transition eg ← t₂g and identifies 20300cm1 with ∆O for the complex. It is not so straightforward to obtain values of ∆O for complexes with more than one d electron because the energy of a transition then depends not only on orbital energies but also on the electron-electron repulsion energies. This aspect is treated more fully in Section 20.4 and the results from the analyses described there have been used to obtain the values of ∆_O in Table 20.1.

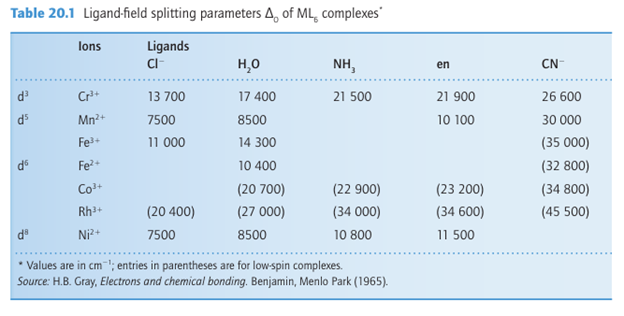
The ligand-field splitting parameter, ∆O , varies systematically with the identity of the lig and. For instance, in the series of complexes [CoX(NH₃)₅]ⁿ with X I, Br, Cl, H₂O, and NH₃, the colours range from purple (for X I ) through pink (for Cl) to yellow (with NH3 ). This sequence indicates that the energy of the lowest energy electronic transition (and therefore ∆_O) increases as the ligands are varied along the series. The same order is followed regardless of the identity of the metal ion. Thus ligands can be arranged in a spectrochemical series, in which the members are arranged in order of increasing energy of transitions that occur when they are present in a complex:

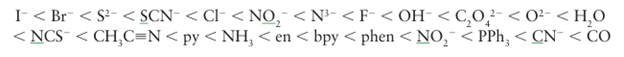
(The donor atom in an ambidentate ligand is underlined.) Thus, the series indicates that, for the same metal, the optical absorption of the cyano complex will occur at higher en ergy than that of the corresponding chlorido complex. A ligand that gives rise to a high energy transition (such as CO) is referred to as a strong-field ligand, whereas one that gives rise to a low-energy transition (such as Br^-) is referred to as a weak-field ligand. Crystal field theory alone cannot explain these strengths, but ligand-field theory can, as we shall see in Section 20.2. The ligand-field strength also depends on the identity of the central metal ion, the order being approximately:

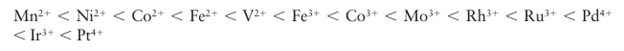
The value of ∆_O increases with increasing oxidation state of the central metal ion (compare the two entries for Fe and Co) and also increases down a group (compare, for instance, the locations of Co, Rh, and Ir). The variation with oxidation state reflects the smaller size of more highly charged ions and the consequently shorter metal ligand distances and stronger interaction energies. The increase down a group reflects the larger size of the 4d and 5d orbitals compared with the compact 3d orbitals and the consequent stronger interactions with the ligands.

اخر الاخبار

اخبار العتبة العباسية المقدسة

جامعة العميد تنظم ورشة تدريبية عن برنامج منصة التعليم العالي

قسم الشؤون الفكرية ينظم برنامجًا دينيًّا لكشافة الكفيل في النجف الأشرف

العتبة العباسية المقدسة تقدم دعوة لجامعتي الكوفة والطوسي للمشاركة في مشروعها القرآني الخاص بطلبة الجامعات

قسم الشؤون الفكرية يصدر مجموعة جديدة من الإصدارات المعرفية والثقافية

المزيد

الآخبار الصحية

كيف يمكن لحفنة من الجوز أن تؤثر على نومك وتركيزك؟

دراسة: كوب ميلك شيك واحد قد يكون "قنبلة دماغية"

هل يعد "الباراسيتامول" خيارا آمنا للنساء الحوامل؟

دراسة تكشف الرابط بين العلاقات العاطفية والرضا عن الحياة

المزيد

الآخبار التكنلوجية

كارثة صامتة.. "الهواء الملوث" يسرق نور عيون الأطفال

دراسة: رصد أول دليل على وجود "إشعاع هوكينغ"

رسالة بلغة لا تعرفها؟.. "واتساب" يترجمها لك فورا

"إنستغرام".. ميزة جديدة لكشف "الكذب في العمر"

المزيد

مواضيع ذات صلة

Thermochemical correlations

Magnetic measurements

Sulfide complexes

Disulfides

Polyoxometallates

Mononuclear oxido complexes

Metal oxides

Structural trends

Oxidation states down a group

Intermediate oxidation states in the 4d and 5d series

Intermediate oxidation states in the 3d series

High oxidation states