Computational techniques

Key point: Computational procedures use either ab initio methods or parametrized semi-empirical methods to calculate the properties of molecules and solids. Graphical techniques can be used to dis play the results. Computation has proved to be one of the most important techniques in chemistry. Computer modelling is the use of numerical models for exploring the structures and prop erties of individual molecules and materials. The methods used range from rigorous, and therefore computationally very time-consuming, treatments, known as ab initio methods, based on the numerical solution of the Schrödinger equation for the system, to the more rapid and necessarily less detailed ‘semi-empirical techniques’, which use approximate or ‘effective functions’ to describe the forces between particles. There are two principal approaches to solving the Schrödinger equation numerically for many-electron polyatomic molecules. In the more fundamental ab initio methods, an attempt is made to calculate structures from first principles, using only the atomic num bers of the atoms present and their general arrangement in space. Such an approach is intrinsically reliable but computationally very demanding. For complex problems involving molecules and materials with numerous atoms, such methods are so computationally time-consuming that alternative methods involving experimental data are needed. In these semi-empirical methods, integrals that occur in the formal solution of the Schrödinger equation are set equal to parameters that have been chosen to lead to the best fit to experimental quantities, such as enthalpies of formation. Semi-empirical methods are applicable to a wide range of molecules with an almost limitless number of atoms, and are widely popular.

Both types of procedure typically adopt a self-consistent field (SCF) procedure, in which an initial guess about the composition of the linear combinations of atomic orbitals (LCAO) used to model molecular orbitals is successively refined until the composition and the corresponding energy remains unchanged in a cycle of calculation. The most common type of ab initio calculation is based on the Hartree–Fock method in which the primary approximation is applied to the electron–electron repulsion. Various methods of correct ing for the explicit electron–electron repulsion, referred to as the correlation problem, are the Møller–Plesset perturbation theory (MPn, where n is the order of correction), the gen eralized valence bond (GVB) method, multi-configurations self-consistent field (MCSCF), configuration interaction (CI), and coupled cluster theory (CC).

A currently popular alternative to the ab initio method is density functional theory (DFT), in which the total energy is expressed in terms of the total electron density P=|Ψ|² rather than the wavefunction itself. When the Schrödinger equation is expressed in terms of ,P, it becomes a set of equations called the Kohn–Sham equations, which are solved iteratively starting from an initial estimate and continuing until they are self-consistent. The advantage of the DFT approach is that it is less demanding computationally, requires less computer time, and—in some cases, particularly d-metal complexes—gives better agreement with experimental values than is obtained from other procedures. Semi-empirical methods are set up in the same general way as Hartree–Fock calculations but within this framework certain pieces of information, such as integrals representing the interaction between two electrons, are approximated by importing empirical data or sim ply ignored. To soften the effect of these approximations, parameters representing other in tegrals are adjusted so as to give the best agreement with experimental data. Semi-empirical calculations are much faster than the ab initio calculations but the quality of results is very dependent on using a reasonable set of experimental parameters that can be transferred from structure to structure. Thus semi-empirical calculations have been very successful in organic chemistry with just a few types of element and molecular geometries. Semi-empirical methods have also been devised specifically for the description of inorganic species. The raw output of a molecular structure calculation is a list of the coefficients of the atomic orbitals in each molecular orbital and the energies of these orbitals. The graphical representation of a molecular orbital uses stylized shapes to represent the basis set and then scales their size to indicate the value of the coefficient in the LCAO. Different signs of the wavefunctions are typically represented by different colours. The total electron density at any point (the sum of the squares of the wavefunctions evaluated at that point) is commonly represented by an isodensity surface, a surface of constant total electron density (Fig. 8.47). An important aspect of a molecule other than its geometrical shape is the distribution of charge over its surface. A common procedure begins with calculation of the net electric potential at each point on an isodensity surface by subtracting the potential due to the electron density at that point from the potential due to the nuclei. The result is an electrostatic potential surface (an ‘elpot surface’) in which net positive potential is shown in one colour and net negative potential is shown in another, with intermediate gradations of colour. Computer modelling is applied to solids as well as to individual molecules and is useful for predicting the behaviour of a material, for example for indicating which crystal struc ture of a compound is energetically most favourable, for predicting phase changes, for calculating thermal expansion coefficients, identifying preferred sites for dopant ions, and calculating a diffusion pathway through a lattice. However, it is worth noting that very few aspects of inorganic chemistry can be computed exactly. Although modelling computation can give a very useful insight into materials chemistry, it is not yet at a stage where it can be used reliably to predict the exact structure or properties of any complex compound.

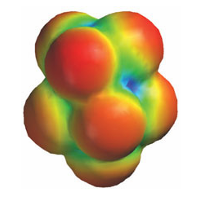
Figure 8.47 The output of computations of the electronic structure of a molecule is conveyed in a variety of ways. Here we show the electric potential surface of SF5 CF₃, a molecule that has been found to act as a very powerful greenhouse gas but of uncertain origin in the atmosphere. Red areas indicate regions of negative potential and green regions of positive potential.

اخر الاخبار

اخبار العتبة العباسية المقدسة

شعبة الخطابة النسوية تطلق العام الدراسي الجديد في معهد الخطابة

صُنع في العراق.. تجربة العتبة العباسية المقدسة في إعادة الهوية المفقودة

قسم الشؤون الفكرية يعلن عن بدء التسجيل للدورة التمهيدية الحوزوية الإلكترونية

أثناء استقباله فريق مجلة (أثر).. سماحة السيد الصافي يؤكد دعم أي إبداع يسهم في تنويع طرائق إيصال المعلومة إلى المتلقي

المزيد

الآخبار الصحية

تحذير من "عدوى بكتيرية" تسبب نوبات قلبية

ماذا يحصل لجسمك عند التوقف عن استخدام الزيت في الطهي؟

الأمل في كبسولة.. "فيتامين شهير" يبطئ التقدم في العمر

اشتهاء أطعمة بشكل مفاجئ.. ناقوس خطر للسرطان ؟!

المزيد

الآخبار التكنلوجية

زلزال أفغانستان يحصد أكثر من ألف قتيل.. ويدمر آلاف المنازل !

ناجٍٍ وحيد من انزلاق أرضي.. دمّر قرية سودانية بأكملها !

نهر الفرات.. مورد مائي بين الندرة والتقاسم

ما السر وراء مشية إيلون ماسك الغريبة والسريعة ؟

المزيد

مواضيع ذات صلة

The atom and its ions

Oxidation states

Occurrence

Enthalpies of atomization

Electronegativity

Ionization energies and electron affinities

Electrochemical techniques

Thermal analysis

X-ray fluorescence elemental analysis

CHN analysis

Atomic absorption spectroscopy

Ionization and detection methods