Vassiliev invariants, discovered around 1989, provided a radically new way of looking at knots. The notion of finite type (a.k.a. Vassiliev) knot invariants was independently invented by V. Vassiliev and M. Goussarov around 1989. Vassiliev's approach is based on the study of discriminants in the (infinite-dimensional) spaces of smooth maps from one manifold into another. By definition, the discriminant consists of all maps with singularities.

For example, consider the space of all smooth maps from the circle into three-space {f:S^1->R^3}" src="https://mathworld.wolfram.com/images/equations/VassilievInvariant/Inline1.gif" style="height:21px; width:109px" />. If 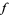 is an embedding (i.e., has no singular points), then it represents a knot. The complement of the set of all knots is the discriminant 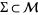. It consists of all smooth maps from  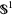into 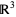 that have singularities, either local, where 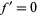, or nonlocal, where  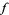is not injective. Two knots are equivalent iff they can be joined by a path in the space  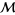that does not intersect the discriminant. Therefore, knot types are in one-to-one correspondence with the connected components of the complement 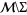, and knot invariants with values in an Abelian group  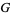are nothing but cohomology classes from 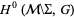. The filtration of  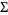by subspaces corresponding to singular knots with a given number of ordinary double points gives rise to a spectral sequence, which contains, in particular, the spaces of finite type invariants.

Birman and Lin (1993) have contributed significantly to the simplification of the Vassiliev's original techniques. In particular, they explained the relation between Jones polynomials and finite type invariants (Peterson 1992, Birman and Lin 1993, Bar-Natan 1995) and emphasized the role of the algebra of chord diagrams. In fact, substituting the power series for 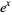 as the variable in the Jones polynomial yields a power series whose coefficients are Vassiliev invariants (Birman and Lin 1993). Kontsevich (1993) proved the first difficult theorem about Vassiliev invariants with the help of the Kontsevich integral. Bar-Natan undertook a thorough study of Vassiliev invariants; in particular, he showed the importance of the algebra of Feynman diagrams and diagrams with uni- and tri-valent vertices (Bar-Natan 1995). Bar-Natan (1995) remains the most authoritative source on the subject.

Expressed in simple terms, Vassiliev's fundamental idea is to study the prolongation of knot invariants to singular knots--immersions 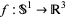 having a finite number of ordinary double points. Let  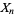denote the set of equivalence classes of singular knots with  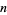double points and no other singularities. The following definition is based on a recursion which allows to extend a knot invariant from  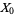to 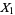, then to 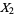, etc., and thus finally to the whole of 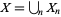. Given a knot invariant 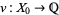, its Vassiliev prolongation  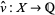is defined as by the rules

1. 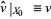, and

2. Vassiliev's skein relation, illustrated below.

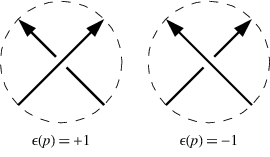
The right-hand side of Vassiliev's skein relation refers to the two resolutions of the double point--positive and negative. A crucial observation is that each of them is well-defined (does not depend on the plane projection used to express this relation). A knot invariant 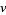 is called a Vassiliev invariant of order  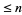if its prolongation  vanishes on all knots with more than 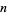 double points. For example, the simplest nontrivial Vassiliev invariant  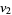has the following explicit description. Let  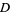be an arbitrary knot diagram of the given knot  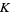and 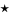 an arbitrary distinguished point on 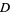, different from all crossings. Then

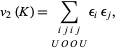where the summation spreads over all pairs of crossing points 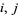 such that (1) during one complete turn of the diagram in the positive direction starting from point  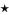the points  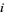and 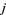 are encountered in the order 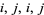, and (2) the four corresponding passages through these crossing points are underpass, overpass, overpass, and underpass, respectively. The numbers 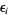,  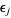stand for the local writhe at points  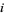and 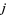, defined according to the above illustration.

It turns out that the 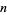th coefficient of the Conway polynomial is a Vassiliev invariant of order  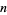and, in particular, the second coefficient coincides with .

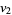Vassiliev invariants are at least as strong as all known polynomial knot invariants: Alexander, Jones, Kauffman, and HOMFLY polynomials. This means that if two knots 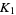 and 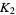 can be distinguished by such a polynomial, then there is a Vassiliev invariant that takes different values for  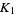and .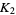

The set of all 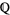-valued Vassiliev invariants  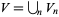forms a vector space over the rationals, with the increasing filtration 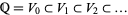. The associated graded space  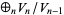has a structure of a Hopf algebra and can be interpreted as the algebra of chord diagrams.

The numbers of independent Vassiliev invariants of a given degree 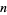 (i.e., the dimension of 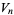) are known for  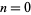to 12 (Kneissler 1997) and are summarized in following table (A007473).

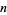	0	1	2	3	4	5	6	7	8	9	10	11	12
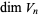	1	1	2	3	6	10	19	33	60	104	184	316	548

The totality of all Vassiliev invariants is equivalent to one universal Vassiliev invariant defined through the Kontsevich integral.

Two of the most important problems about Vassiliev invariants were raised in 1990 and remain unanswered today.

1. Is it true that Vassiliev invariants distinguish knots? In other words, given two nonequivalent knots 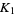 and 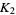, is it always possible to indicate a finite type invariant  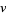such that ?

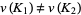2. Is it true that Vassiliev invariants can detect knot orientation? More specifically, is there a knot 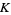 and a finite type invariant  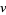such that 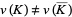, where  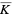differs from  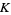by a change of parameterization that reverses the orientation?

REFERENCES:

Bar-Natan, D. "Bibliography of Vassiliev Invariants." https://www.ma.huji.ac.il/~drorbn/VasBib/VasBib.html.

Bar-Natan, D. "On the Vassiliev Knot Invariants." Topology 34, 423-472, 1995.

Birman, J. S. "New Points of View in Knot Theory." Bull. Amer. Math. Soc. 28, 253-287, 1993.

Birman, J. S. and Lin, X.-S. "Knot Polynomials and Vassiliev's Invariants." Invent. Math. 111, 225-270, 1993.

Duzhin, S. V. "Vassiliev Invariants and Combinatorial Structures." Lectures delivered at Graduate School of Mathematical Sciences, University of Tokyo, April-July 1999. https://www.pdmi.ras.ru/~duzhin/Vics/.

Goussarov, M. "On 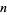-Equivalence of Knots and Invariants of Finite Degree." In Topology of Manifolds and Varieties (Ed. O. Viro). Providence, RI: Amer. Math. Soc., pp. 173-192, 1994.

Kneissler, J. "The Number of Primitive Vassiliev Invariants up to Degree Twelve." 1997. https://www.math.uni-bonn.de/people/jk/papers/pvi12.pdf.gz.

Kontsevich, M. "Vassiliev's Knot Invariants." Adv. Soviet Math. 16, Part 2, pp. 137-150, 1993.

Peterson, I. "Knotty Views: Tying Together Different Ways of Looking at Knots." Sci. News 141, 186-187, 1992.

PaliMathov, V. V. and Sossinsky, A. B. Knots, Links, Braids and 3-Manifolds: An Introduction to the New Invariants in Low-Dimensional Topology. Providence, RI: Amer. Math. Soc., 1996.

Sloane, N. J. A. Sequence A007473/M0765 in "The On-Line Encyclopedia of Integer Sequences."

Stoimenow, A. "Degree-3 Vassiliev Invariants." https://www.ms.u-tokyo.ac.jp/~stoimeno/ptab/vas3.html.

Vassiliev, V. A. "Cohomology of Knot Spaces." In Theory of Singularities and Its Applications (Ed. V. I. Arnold). Providence, RI: Amer. Math. Soc., pp. 23-69, 1990.

Vassiliev, V. A. Complements of Discriminants of Smooth Maps: Topology and Applications. Providence, RI: Amer. Math. Soc., 1992.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الدينية يُطلق دورة فقهية دينية لملاكات مستشفى الكفيل

شعبة فاطمة بنت أسد للدراسات القرآنية تعلن نتائج مسابقة (ميثاق الرسول)

شعبة الخطابة الحسينية النسوية تنظّم مسابقة فرقية لطالبات برنامج ثمار العطاء

قسم العلاقات ينظم ورشة عن فن الإقناع والتواصل الفعّال للطلبة المنسقين

المزيد

الآخبار الصحية

تغيير بسيط في نمط التفكير قد يحدث فرقا كبيرا لصحة الدماغ ؟

لماذا ينعشنا المشروب الساخن في الطقس الحار؟

علماء يكتشفون فئة دم فريدة من نوعها في العالم !

لماذا ينصح الأطباء بزيت الزيتون يوميا؟

المزيد

الآخبار التكنلوجية

حساس الإطارات.. ما هو وعلامات تلفه وكيفية صيانته؟

ما معنى أودي Quattro؟ سر الأداء والتميز الهندسي ؟!

فصل الشاحن أم الهاتف أولا؟.. عادات بسيطة تطيل عمر البطارية

تعود للقرن الرابع قبل الميلاد.. اكتشاف بقايا "إيمت" المصرية

المزيد