Braid Group
المؤلف:
Adams, C. C.
المصدر:
The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman
الجزء والصفحة:
...
6-6-2021
2735
Braid Group
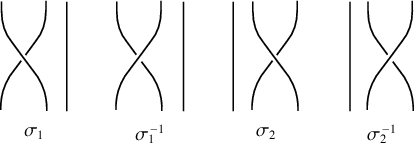
Consider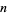 
strings, each oriented vertically from a lower to an upper "bar." If this is the least number of strings needed to make a closed braid representation of a link, 
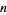is called the braid index. A general 
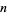-braid is constructed by iteratively applying the 
(
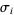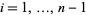) operator, which switches the lower endpoints of the 
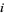th and 
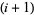th strings--keeping the upper endpoints fixed--with the 
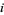th string brought above the 
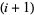th string. If the 
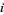th string passes below the 
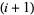th string, it is denoted 
.
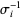The operations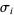 
and 
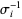on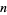 
strings define a group known as the braid group or Artin braid group, denoted 
.
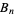Topological equivalence for different representations of a braid wor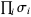d 
and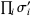 
is guaranteed by the conditions
![<span style=]() {sigma_isigma_j=sigma_jsigma_i for |i-j|>=2; sigma_isigma_(i+1)sigma_i=sigma_(i+1)sigma_isigma_(i+1) for all i " src="https://mathworld.wolfram.com/images/equations/BraidGroup/NumberedEquation1.gif" style="height:44px; width:246px" /> |
(1)
|
as first proved by E. Artin.
Any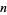 
-braid can be expressed as a braid word, e.g., 
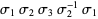is a braid word in the braid group 
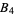. When the opposite ends of the braids are connected by nonintersecting lines, knots (or links) may formed that can be labeled by their corresponding braid word. The Burau representation gives a matrix representation of the braid groups.
REFERENCES:
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 132-133, 1994.
Birman, J. S. "Braids, Links, and the Mapping Class Groups." Ann. Math. Studies, No. 82. Princeton, NJ: Princeton University Press, 1976.
Birman, J. S. "Recent Developments in Braid and Link Theory." Math. Intell. 13, 52-60, 1991.
Christy, J. "Braids." http://library.wolfram.com/infocenter/MathSource/813/.
Jones, V. F. R. "Hecke Algebra Representations of Braid Groups and Link Polynomials." Ann. Math. 126, 335-388, 1987.
Murasugi, K. and Kurpita, B. I. A Study of Braids. Dordrecht, Netherlands: Kluwer, 1999.
الاكثر قراءة في التبلوجيا
اخر الاخبار
اخبار العتبة العباسية المقدسة
