Temperature
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص5-7
2025-10-29
35
Temperature
The concept of temperature springs from the observation that a change in physical state (for example, a change of volume) can occur when two objects are in contact with one another, as when a red-hot metal is plunged into water. Later (Section 2.1) we shall see that the change in state can be interpreted as arising from a flow of energy as heat from one object to another. The temperature, T, is the property that indicates the direction of the flow of energy through a thermally conducting, rigid wall. If energy flows from A to B when they are in contact, then we say that A has a higher temperature than B (Fig. 1.2). It will prove useful to distinguish between two types of boundary that can separate the objects. A boundary is diathermic (thermally conducting) if a change of state is observed when two objects at different temperatures are brought into contact.1 A metal container has diathermic walls. A boundary is adiabatic (thermally insulating) if no change occurs even though the two objects have different temperatures. A vacuum flask is an approximation to an adiabatic container.
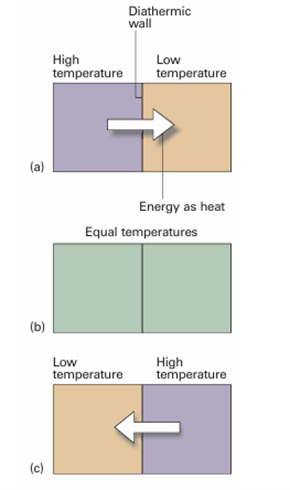
Fig. 1.2 Energy flows as heat from a region at a higher temperature to one at a lower temperature if the two are in contact through a diathermic wall, as in (a) and (c). However, if the two regions have identical temperatures, there is no net transfer of energy as heat even though the two regions are separated by a diathermic wall (b). The latter condition corresponds to the two regions being at thermal equilibrium.
The temperature is a property that indicates whether two objects would be in ‘thermal equilibrium’ if they were in contact through a diathermic boundary. Thermal equilibrium is established if no change of state occurs when two objects A to B are in contact through a diathermic boundary. Suppose an object A (which we can think of as a block of iron) is in thermal equilibrium with an object B (a block of copper), and that B is also in thermal equilibrium with another object C (a flask of water). Then it has been found experimentally that A and C will also be in thermal equilibrium when they are put in contact (Fig. 1.3). This observation is summarized by the Zeroth Law of thermodynamics:
If A is in thermal equilibrium with B, and B is in thermal equilibrium with C, then C is also in thermal equilibrium with A.
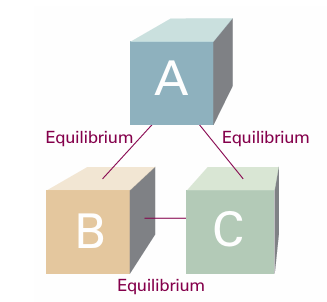
Fig. 1.3 The experience summarized by the Zeroth Law of thermodynamics is that, if an object A is in thermal equilibrium with B and B is in thermal equilibrium with C, then C is in thermal equilibrium with A.
The Zeroth Law justifies the concept of temperature and the use of a thermometer, a device for measuring the temperature. Thus, suppose that B is a glass capillary containing a liquid, such as mercury, that expands significantly as the temperature increases. Then, when A is in contact with B, the mercury column in the latter has a certain length. According to the Zeroth Law, if the mercury column in B has the same length when it is placed in thermal contact with another object C, then we can predict that no change of state of A and C will occur when they are in thermal contact. More-over, we can use the length of the mercury column as a measure of the temperatures of A and C. In the early days of thermometry (and still in laboratory practice today), tempera tures were related to the length of a column of liquid, and the difference in lengths shown when the thermometer was first in contact with melting ice and then with boiling water was divided into 100 steps called ‘degrees’, the lower point being labelled 0. This procedure led to the Celsius scale of temperature. In this text, temperatures on the Celsius scale are denoted θ and expressed in degrees Celsius (°C). However, because different liquids expand to different extents, and do not always expand uniformly over a given range, thermometers constructed from different materials showed different numerical values of the temperature between their fixed points. The pressure of a gas, however, can be used to construct a perfect-gas temperature scale that is independent of the identity of the gas. The perfect-gas scale turns out to be identical to the thermodynamic temperature scale to be introduced in Section 3.2c, so we shall use the latter term from now on to avoid a proliferation of names. On the thermodynamic temperature scale, temperatures are denoted T and are normally reported in kelvins, K (not °K). Thermodynamic and Celsius temperatures are related by the exact expression
T/K=θ/°C + 273.15
This relation, in the form θ/°C = T/K − 273.15, is the current definition of the Celsius scale in terms of the more fundamental Kelvin scale. It implies that a difference in temperature of 1°C is equivalent to a difference of 1 K.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
