1. f is called onto or surjective if codom f = ran f. If f is surjective, we sometimes indicate this by writing f : A ։ B.

2. f is called one–one or injective if for all x, y ∈ A, f(x) = f(y) implies x = y. If f is injective, we sometimes indicate this by writing f : A → B.

3. f is called bijective if f is onto and one-one.

Thus, f is onto if, in the pictorial representation, at least one arrow arrives at every element of the codomain; in other words, for every y ∈ codom f there exists at least one element x of dom f with f(x) = y. If f is one–one, then at most one arrow arrives at every element of codom f. If f is bijective, then exactly one arrow arrives at every element of codom f, see Figure 1.1.

Figure 1.1: Types of functions

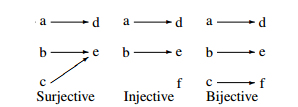
Example 1.1.

1. f : R → R, f(x) = 2x:

f is one–one: We have to show that for all x,y ∈ R,f(x) = f(y) implies x = y. So let f(x) = f(y); by definition of f, f(x) = 2x and f(y) = 2y.

         Since f(x) = f(y), the definition of f tells us that 2x = 2y, which implies x = y.

f is onto: For every real number y we have to find a real number x such that f(x) = y, which, by our definition of f is the same as 2x = y. Solving this equation for x gives us x =y/2; so, f(y/2) = y.

Since f is one–one and onto, it is bijective.

2. f : R → R, f(x) = x²:

f is not one–one: To show that an object does not have a certain property, it is enough to exhibit one counterexample, So, to show that f is not one–one we have to find two different real numbers x and y such that f(x) = f(y).

This is easily done by choosing x = 1 and y = −1.

f is not onto: Again, we have to find just one counterexample. If e.g. y = −1, then for no real number x we have f(x) = y, since the square of a real number is never negative.

3. Let R⁺ be the set of positive real numbers and define f : R → R⁺ by f(x) = x².

Observe that we have only changed the codomain of the previous example. The function still is not one–one, but now it is onto, since every positive real number is a square.

4. Let f : R⁺ → R be defined by f(x) = x².

We have only changed the domain of f from Example 2. This function is not onto – the codomain is still all of R, and negative numbers still cannot be squares of real numbers.

But our new f is one–one, since every real number has at most one positive root.

These examples tell us that the properties of being one–one or onto depend not only on the rule of assignment, but also on the domain and the codomain of the function. In fact, by changing the codomain of a function, we can always obtain a surjective function with the same domain and the same rule of assignment:

Lemma 1.1. Let f : A → B be a function; then g : A → ran f defined by g(x) = f(x) for all x ∈ A is onto.

Proof. Since dom f = dom g, and g(x) = f(x) for all x ∈ A, g is a function. To show that g is onto, let y ∈ codom g. By our definition of g, codom g = ran f;  thus there is an x ∈ A = dom f such that f(x) = y. Now, since dom f = dom g we have x ∈ dom g; furthermore, since f(x) = g(x), we obtain g(x) = y. This shows that g is onto.

Each function f : A → B can be written as a composition f = h ◦ g of functions,  where g is surjective, and h is injective. This is an important Theorem which is used in many algebraic contexts. To prepare for a proof, we need

Definition 1.2. Let f : A → B be a function. Then the canonical equivalence relation θ_f of f is defined by

                           xθ_{f y} ⇐⇒ f(x) = f(y)

for all x,y ∈ A.

The set {θ_fx : x ∈ A} of equivalence classes of θ_f is called the quotient set of A with respect to f, written as A/θf , or simply quotient set, if f is understood.

Theorem 1.2. Let f : A → B be a function. Then, there are a set C, and functions g : A ։ C, h : C→ B such that g is surjective, h is injective, and f = h ◦ g.

The situation is picture in Figure 1.2

Figure 1.2: Mapping Theorem

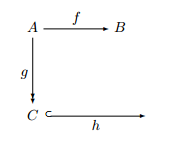
Proof. Set C = A/θ_f , and letg : A → A/θ_f be defined by x ^g→ θ_fx. Since each element of A is contained in exactly one class of E(θ_f ), h is a surjective function.

Now, let h : A/θ_f → B be defined as follows: Let t ∈ A/θ_f . Then, there is some x ∈ A, such that t = θfx; set h(t) = f(x). We need to show that the definition of h is independent of the choice of the representative x of the class t. Thus, let y ∈ θ_fx. By definition of θ_f , we have xθ_f y if and only if f(x) = f(y), and it follows that f(y) = f(x) for all y ∈ θ_fx.

Finally,

(g ◦ h)(x) = g(θfx) = f(x),

اخر الاخبار

اخبار العتبة العباسية المقدسة

المجمع العلمي يحتفي بذكرى ولادة الإمامين الباقر والهادي (عليهما السلام)

قسم الشؤون الفكرية يطلق فعاليات الأسبوع الثالث من برنامج البذرة الصالحة

تكريم الفائزين في المسابقة الثقافية الخاصّة بذكرى ولادة الإمامين الباقر والهادي (عليهما السلام)

بذكرى ولادتهما.. العتبة العباسية المقدسة تستذكر السيرة العطرة للإمامين الباقر والهادي (عليهما السلام)

المزيد

الآخبار الصحية

ثورة طبية.. الذكاء الاصطناعي يكشف سرطان الكلى في وقت قياسي

لتعزيز الطاقة والتغلب على التعب.. عليك بـ7 طرق بسيطة

لتحسين الهضم والتحكم في الشهية.. ما أفضل وقت لتناول التمر؟

خبراء يكشفون تأثير الاستحمام في الظلام على جودة النوم !

المزيد

الآخبار التكنلوجية

إزالة ثاني أكسيد الكربون من الغلاف الجوي.. ما دور المحيطات والبحار؟

نظائر الهيليوم مقياس لاكتشاف رواسب الذهب.. كيف ذلك؟

الصين تطلق أول ناقلة نفط خام ذكية في العالم تعمل بالميثانول

الزمن على المريخ أسرع من الأرض.. دراسة علمية تكشف الفوارق

المزيد

مواضيع ذات صلة

Subset

Set Class

Set

Second Category

Proper Subset

Power Set

Matroid

Inductive Set

Independent Vertex Set

Independent Set

Graphoid

G_delta Set