The thermodynamic definition of entropy
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص78-80
2025-11-04
53
The thermodynamic definition of entropy
The thermodynamic definition of entropy concentrates on the change in entropy, dS, that occurs as a result of a physical or chemical change (in general, as a result of a ‘process’). The definition is motivated by the idea that a change in the extent to which energy is dispersed depends on how much energy is transferred as heat. As we have remarked, heat stimulates random motion in the surroundings. On the other hand, work stimulates uniform motion of atoms in the surroundings and so does not change their entropy. The thermodynamic definition of entropy is based on the expression , dS = dqrev /T , For a measurable change between two states i and f this expression integrates to
That is, to calculate the difference in entropy between any two states of a system, we find a reversible path between them, and integrate the energy supplied as heat at each stage of the path divided by the temperature at which heating occurs.
We can use the definition in eqn 3.1 to formulate an expression for the change in entropy of the surroundings, ∆Ssur. Consider an infinitesimal transfer of heat dqsur to the surroundings. The surroundings consist of a reservoir of constant volume, so the energy supplied to them by heating can be identified with the change in their internal energy, dUsur.3 The internal energy is a state function, and dUsur is an exact differential. As we have seen, these properties imply that dUsur is independent of how the change is brought about and in particular is independent of whether the process is reversible or irreversible. The same remarks therefore apply to dqsur, to which dUsur is equal. Therefore, we can adapt the definition in eqn 3.1 to write
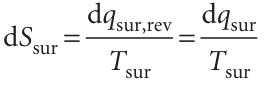
Furthermore, because the temperature of the surroundings is constant whatever the change, for a measurable change
∆Ssur = qsur/Tsur
That is, regardless of how the change is brought about in the system, reversibly or irreversibly, we can calculate the change of entropy of the surroundings by dividing the heat transferred by the temperature at which the transfer takes place. Equation 3.3 makes it very simple to calculate the changes in entropy of the surround ings that accompany any process. For instance, for any adiabatic change, qsur = 0, so For an adiabatic change: ∆Ssur = 0 .
This expression is true however the change takes place, reversibly or irreversibly, provided no local hot spots are formed in the surroundings. That is, it is true so long as the surroundings remain in internal equilibrium. If hot spots do form, then the localized energy may subsequently disperse spontaneously and hence generate more entropy.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
