Changes in internal energy at constant pressure
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص61-63
2025-11-04
59
Changes in internal energy at constant pressure
Partial derivatives have many useful properties and some that we shall draw on frequently are reviewed in Appendix 2. Skilful use of them can often turn some unfamiliar quantity into a quantity that can be recognized, interpreted, or measured. As an example, suppose we want to find out how the internal energy varies with temperature when the pressure of the system is kept constant. If we divide both sides of eqn 2.42 by dT and impose the condition of constant pressure on the resulting differentials, so that dU/dT on the left becomes (∂U/∂T)p, we obtain
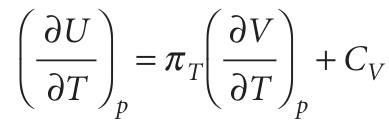
It is usually sensible in thermodynamics to inspect the output of a manipulation like this to see if it contains any recognizable physical quantity. The partial derivative on the right in this expression is the slope of the plot of volume against temperature (at constant pressure). This property is normally tabulated as the expansion coefficient, α, of a substance,7 which is defined as
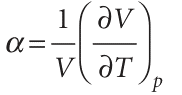
and physically is the fractional change in volume that accompanies a rise in temperature. A large value of α means that the volume of the sample responds strongly to changes in temperature. Table 2.8 lists some experimental values of α and of the isothermal compressibility, κT (kappa), which is defined as
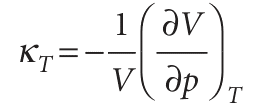
The isothermal compressibility is a measure of the fractional change in volume when the pressure is increased by a small amount; the negative sign in the definition ensures that the compressibility is a positive quantity, because an increase of pressure, implying a positive dp, brings about a reduction of volume, a negative dV.
When we introduce the definition of α into the equation for (∂U/∂T)p, we obtain
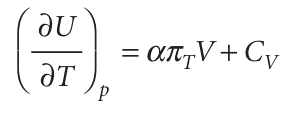
This equation is entirely general (provided the system is closed and its composition is constant). It expresses the dependence of the internal energy on the temperature at constant pressure in terms of CV, which can be measured in one experiment, in terms of α, which can be measured in another, and in terms of the quantity πT. For a perfect gas, πT = 0, so then
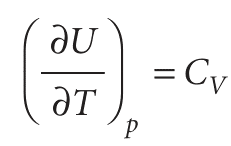
As for heat capacities, the expansion coefficients of a mixture depends on whether or not the composition is allowed to change. Throughout this chapter, we deal only with pure substances, so this complication can be disregarded.
That is, although the constant-volume heat capacity of a perfect gas is defined as the slope of a plot of internal energy against temperature at constant volume, for a perfect gas CV is also the slope at constant pressure. Equation 2.46 provides an easy way to derive the relation between Cp and CV for a perfect gas expressed in eqn 2.26. Thus, we can use it to express both heat capacities in terms of derivatives at constant pressure:
Then we introduce H=U+pV=U+nRT into the first term, which results in
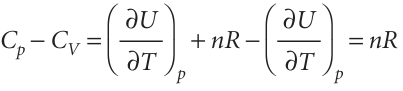
which is eqn 2.26. We show in Further information2.2that in general
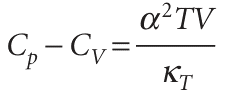
Equation 2.49 applies to any substance (that is, it is ‘universally true’). It reduces to eqn 2.48 for a perfect gas when we set α=1/T and κT=1/p. Because expansion coefficientsαof liquids and solids are small, it is tempting to deduce from eqn 2.49 that for them Cp≈CV. But this is not always so, because the compressibility κT might also be small, so α2/κT might be large. That is, although only a little work need be done to push back the atmosphere, a great deal of work may have to be done to pull atoms apart from one another as the solid expands. As an illustration, for water at 25°C, eqn 2.49 gives Cp,m=75.3 J K−1mol−1compared with CV,m=74.8 J K−1mol−1. In some cases, the two heat capacities differ by as much as 30 per cent.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
