General considerations
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص59-60
2025-11-04
51
General considerations
When V changes to V +dV at constant temperature, U changes to
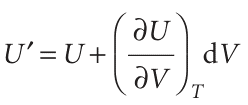
The coefficient (∂U/∂V) T, the slope of a plot of U against V at constant temperature, is the partial derivative of U with respect to V (Fig. 2.21). If, instead, T changes to T + dT at constant volume (Fig. 2.22), then the internal energy changes to
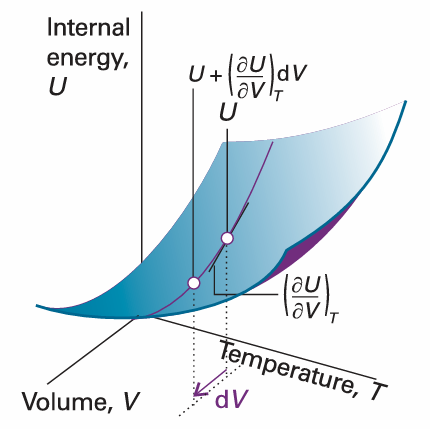
Fig. 2.21 The partial derivative (∂U/∂V) T is the slope of U with respect to V with the temperature T held constant.
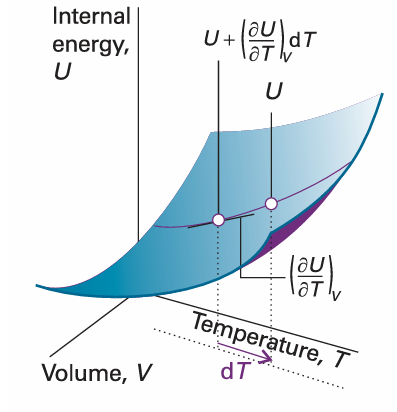
Fig. 2.22 The partial derivative (∂U/∂T) V is the slope of U with respect to T with the volume V held constant.
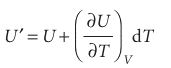
Now suppose that V and T both change infinitesimally (Fig. 2.23). The new internal energy, neglecting second-order infinitesimals (those proportional to dV dT), is the sum of the changes arising from each increment:
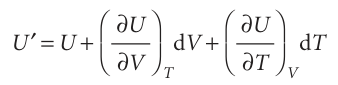
As a result of the infinitesimal changes in conditions, the internal energy U′ differs from U by the infinitesimal amount dU, so we an write U′=U + dU. Therefore, from the last equation we obtain the very important result that
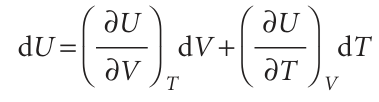
The interpretation of this equation is that, in a closed system of constant composition, any infinitesimal change in the internal energy is proportional to the infinitesimal changes of volume and temperature, the coefficients of proportionality being the two partial derivatives. In many cases partial derivatives have a straightforward physical interpretation, and thermodynamics gets shapeless and difficult only when that interpretation is not kept in sight. In the present case, we have already met (∂U/∂T) V in eqn 2.15, where we saw that it is the constant-volume heat capacity, CV. The other coefficient, (∂U/∂V) T, plays a major role in thermodynamics because it is a measure of the variation of the internal energy of a substance as its volume is changed at constant temperature (Fig. 2.24). We shall denote it πT and, because it has the same dimensions as pressure, call it the internal pressure:
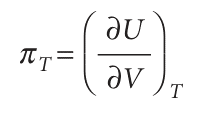
In terms of the notation CV and πT, eqn 2.40 can now be written
dU=πTdV +CVdT
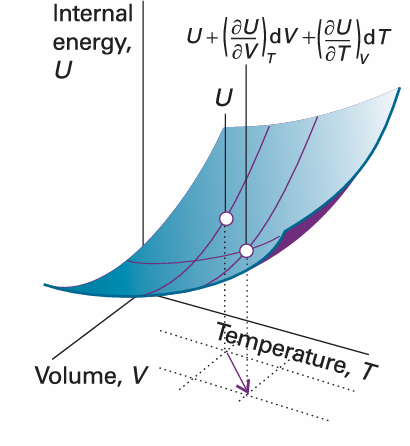
Fig. 2.23 An overall change in U, which is denoted dU, arises when both V and T are allowed to change. If second-order infinitesimals are ignored, the overall change is the sum of changes for each variable separately.
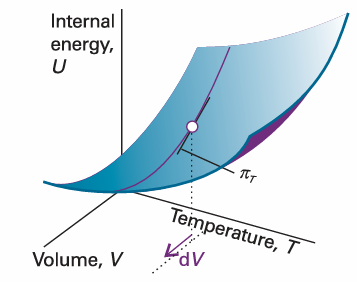
Fig. 2.24 The internal pressure, πT, is the slope of U with respect to V with the temperature T held constant.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
