Hasse Diagram
المؤلف:
Skiena, S.
المصدر:
Hasse Diagrams." §5.4.2 in Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley
الجزء والصفحة:
p. 163, 169-170, and 206-208
5-1-2022
1592
Hasse Diagram
A Hasse diagram is a graphical rendering of a partially ordered set displayed via the cover relation of the partially ordered set with an implied upward orientation. A point is drawn for each element of the poset, and line segments are drawn between these points according to the following two rules:
1. If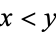 
in the poset, then the point corresponding to 
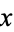appears lower in the drawing than the point corresponding to 
.
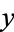2. The line segment between the points corresponding to any two elements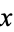 
and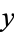 
of the poset is included in the drawing iff 
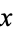covers 
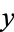or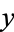 
covers 
.
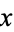Hasse diagrams are also called upward drawings. Hasse diagrams for a graph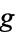 
are implemented as HasseDiagram[g] in the Wolfram Language package Combinatorica` , where 
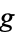is a directed acyclic Combinatorica graph object.
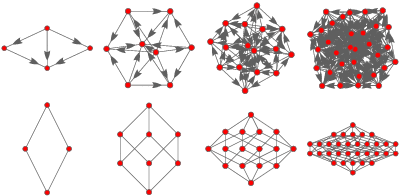
The above figures show the Hasse diagrams for Boolean algebras of orders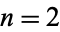 
, 3, 4, and 5. In particular, these figures illustrate the partition between left and right halves of the lattice, each of which is the Boolean algebra on 
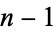elements (Skiena 1990, pp. 169-170). These correspond precisely to the hypercube graphs 
.
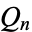REFERENCES:
Skiena, S. "Hasse Diagrams." §5.4.2 in Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, p. 163, 169-170, and 206-208, 1990.
الاكثر قراءة في نظرية المجموعات
اخر الاخبار
اخبار العتبة العباسية المقدسة
