Locally Bounded Lattice
المؤلف:
Grätzer, G
المصدر:
Lattice Theory: First Concepts and Distributive Lattices. San Francisco, CA: W. H. Freeman, 1971.
الجزء والصفحة:
...
2-1-2022
1852
Locally Bounded Lattice
A lattice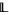 
is locally bounded if and only if each of its finitely generated sublattices is bounded.
Every locally bounded lattice is locally subbounded, and every locally bounded lattice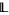 
has a bounded hyperfinite extension in any nonstandard enlargement 
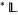. This latter nonstandard property characterizes locally subbounded lattices.
A locally bounded lattice is locally tight if and only if each of its hyperfinitely generated extensions is internally tight. One can also prove the following result, using nonstandard characterizations of these notions: Let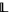 
be a locally finite lattice with at least one strictly increasing meet endomorphism and at least one strictly decreasing join endomorphism. If 
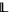is locally tight, then it is bounded.
REFERENCES:
Grätzer, G. Lattice Theory: First Concepts and Distributive Lattices. San Francisco, CA: W. H. Freeman, 1971.
Hobby, D. and McKenzie, R. The Structure of Finite Algebras. Providence, RI: Amer. Math. Soc., 1988.
Insall, M. "Some Finiteness Conditions in Lattices Using Nonstandard Proof Methods." J. Austral. Math. Soc. 53, 266-280, 1992.
الاكثر قراءة في نظرية المجموعات
اخر الاخبار
اخبار العتبة العباسية المقدسة
