Hausdorff Dimension
المؤلف:
Duvall, P.; Keesling, J.; and Vince, A.
المصدر:
"The Hausdorff Dimension of the Boundary of a Self-Similar Tile." J. London Math
الجزء والصفحة:
...
19-9-2021
3837
Hausdorff Dimension
Informally, self-similar objects with parameters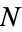 
and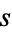 
are described by a power law such as
where
is the "dimension" of the scaling law, known as the Hausdorff dimension.
Formally, let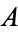 
be a subset of a metric space 
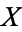. Then the Hausdorff dimension 
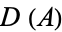of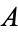 
is the infimum of 
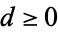such that the 
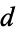-dimensional Hausdorff measure of 
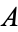is 0 (which need not be an integer).
In many cases, the Hausdorff dimension correctly describes the correction term for a resonator with fractal perimeter in Lorentz's conjecture. However, in general, the proper dimension to use turns out to be the Minkowski-Bouligand dimension (Schroeder 1991).
REFERENCES:
Duvall, P.; Keesling, J.; and Vince, A. "The Hausdorff Dimension of the Boundary of a Self-Similar Tile." J. London Math. Soc. 61, 649-760, 2000.
Federer, H. Geometric Measure Theory. New York: Springer-Verlag, 1969.
Harris, J. W. and Stocker, H. "Hausdorff Dimension." §4.11.3 in Handbook of Mathematics and Computational Science. New York: Springer-Verlag, pp. 113-114, 1998.
Hausdorff, F. "Dimension und äußeres Maß." Math. Ann. 79, 157-179, 1919.
Ott, E. "Appendix: Hausdorff Dimension." Chaos in Dynamical Systems. New York: Cambridge University Press, pp. 100-103, 1993.
Schroeder, M. Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. New York: W. H. Freeman, pp. 41-45, 1991.
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
