The Hénon-Heiles equation is a nonlinear nonintegrable Hamiltonian system with

			(1)
			(2)

where the potential energy function is defined by the polar equation

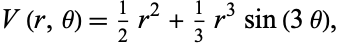(3)

giving Cartesian potential

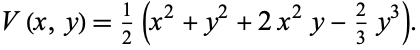(4)

The total energy of the system is then given by

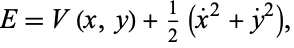(5)

which is conserved during motion.

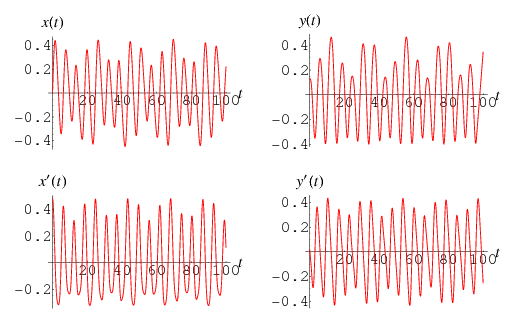
Integrating the above coupled ordinary differential equations from an arbitrary starting point with 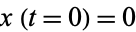 and 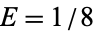 gives the motion illustrated above.

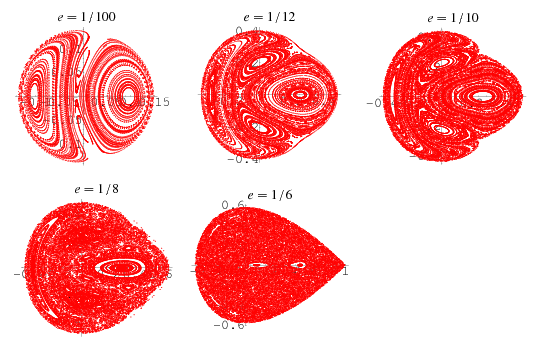
Surfaces of section are illustrated above for various initial energies 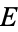,  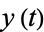is plotted vs.  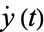at values where .

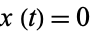The Hamiltonian for a generalized Hénon-Heiles potential is

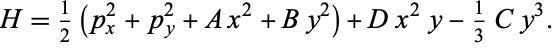(6)

The equations of motion are integrable only for

1. ,

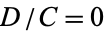2. ,

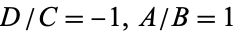3. 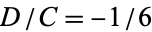, and

4. .

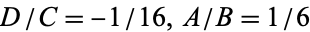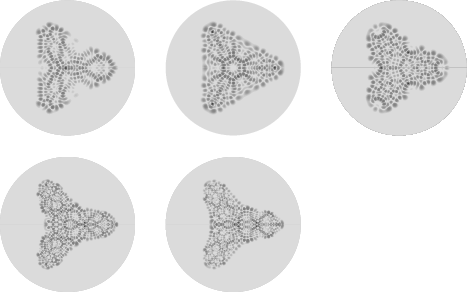
The plots above show a number of eigenfunctions of the Schrödinger equation with a generalized Hénon-Heiles potential

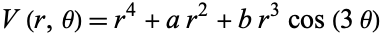(7)

for certain specific values of 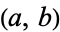 (M. Trott, pers. comm., Jan. 6, 2004).

REFERENCES:

Gleick, J. Chaos: Making a New Science. New York: Penguin Books, pp. 144-153, 1988.

Hénon, M. and Heiles, C. "The Applicability of the Third Integral of Motion: Some Numerical Experiments." Astron. J. 69, 73-79, 1964.

Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 171-172, 1990.

Tabor, M. "The Hénon-Heiles Hamiltonian." §4.1.b in Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, pp. 121-122, 1989.

Trott, M. "The Mathematica Guidebooks Additional Material: Hénon-Heiles Eigenfunctions." http://www.mathematicaguidebooks.org/additions.shtml#S_2_01.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الدينية يُطلق دورة فقهية دينية لملاكات مستشفى الكفيل

شعبة فاطمة بنت أسد للدراسات القرآنية تعلن نتائج مسابقة (ميثاق الرسول)

شعبة الخطابة الحسينية النسوية تنظّم مسابقة فرقية لطالبات برنامج ثمار العطاء

قسم العلاقات ينظم ورشة عن فن الإقناع والتواصل الفعّال للطلبة المنسقين

المزيد

الآخبار الصحية

تغيير بسيط في نمط التفكير قد يحدث فرقا كبيرا لصحة الدماغ ؟

لماذا ينعشنا المشروب الساخن في الطقس الحار؟

علماء يكتشفون فئة دم فريدة من نوعها في العالم !

لماذا ينصح الأطباء بزيت الزيتون يوميا؟

المزيد

الآخبار التكنلوجية

حساس الإطارات.. ما هو وعلامات تلفه وكيفية صيانته؟

ما معنى أودي Quattro؟ سر الأداء والتميز الهندسي ؟!

فصل الشاحن أم الهاتف أولا؟.. عادات بسيطة تطيل عمر البطارية

تعود للقرن الرابع قبل الميلاد.. اكتشاف بقايا "إيمت" المصرية

المزيد