A totalistic cellular automaton is a cellular automata in which the rules depend only on the total (or equivalently, the average) of the values of the cells in a neighborhood. These automata were introduced by Wolfram in 1983. Like an elementary cellular automaton, the evolution of a one-dimensional totalistic cellular automaton can completely be described by a table specifying the state a given cell will have in the next generation based on the average value of the three cells consisting of the cell to its left, the value the cell itself, and the value of the cell to its right.

For a 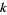-color one-dimensional totalistic automaton, there are  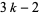possible states for the average of three cells neighboring a given cell, and a total of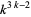 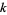 -color totalistic cellular automata, each of which can be indexed with an 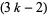-digit 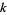-ary number, known as a "code." For example, the table giving the evolution of the 3-color code  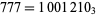is illustrated above. In this diagram, the possible average values of the three neighboring cells are shown in the top row of each panel, and the resulting value the central cell takes in the next generation is shown below in the center.  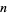generations of the totalistic cellular automaton code  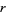with 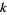 colors is implemented in as CellularAutomaton[{" src="https://mathworld.wolfram.com/images/equations/TotalisticCellularAutomaton/Inline11.gif" style="height:15px; width:5px" />r, {" src="https://mathworld.wolfram.com/images/equations/TotalisticCellularAutomaton/Inline12.gif" style="height:15px; width:5px" />3, 1}" src="https://mathworld.wolfram.com/images/equations/TotalisticCellularAutomaton/Inline13.gif" style="height:15px; width:5px" />}" src="https://mathworld.wolfram.com/images/equations/TotalisticCellularAutomaton/Inline14.gif" style="height:15px; width:5px" />, {" src="https://mathworld.wolfram.com/images/equations/TotalisticCellularAutomaton/Inline15.gif" style="height:15px; width:5px" />{" src="https://mathworld.wolfram.com/images/equations/TotalisticCellularAutomaton/Inline16.gif" style="height:15px; width:5px" />1}" src="https://mathworld.wolfram.com/images/equations/TotalisticCellularAutomaton/Inline17.gif" style="height:15px; width:5px" />, 0}" src="https://mathworld.wolfram.com/images/equations/TotalisticCellularAutomaton/Inline18.gif" style="height:15px; width:5px" />, n, {" src="https://mathworld.wolfram.com/images/equations/TotalisticCellularAutomaton/Inline19.gif" style="height:15px; width:5px" />All, All}" src="https://mathworld.wolfram.com/images/equations/TotalisticCellularAutomaton/Inline20.gif" style="height:15px; width:5px" />].

The evolution of a one-dimensional cellular automaton can be illustrated by starting with the initial state (generation zero) in the first row, the first generation on the second row, and so on. For example, the figures above illustrate the first 20 generations of the code 777 3-color totalistic cellular automaton starting with a single gray cell (left figure) and a single black cell (right figure).

The illustrations above show automata numbers 600, 777, 993, 1020, 1074, and 1083 propagated for 25 generations.

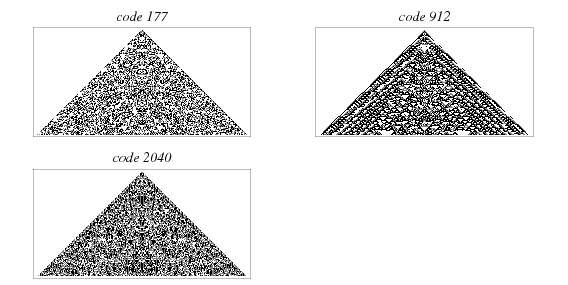
The illustrations above show one-dimensional automata that display apparently random features.

The best known two-dimensional totalistic cellular automaton is the game of life.

REFERENCES:

 Rangel-Mondragon, J. "A Catalog of Cellular Automata." http://library.wolfram.com/infocenter/MathSource/505/.

Wolfram, S. "Statistical Mechanics of Cellular Automata." Rev. Mod. Phys. 55, 601-644, 1983.

Wolfram, S. "Universality and Complexity in Cellular Automata." Physica D 10, 1-35, 1984.

Wolfram, S. "Twenty Problems in the Theory of Cellular Automata." Physica Scripta T9, 170-183, 1985.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 60-70 and 886, 2002.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الدينية يُطلق دورة فقهية دينية لملاكات مستشفى الكفيل

شعبة فاطمة بنت أسد للدراسات القرآنية تعلن نتائج مسابقة (ميثاق الرسول)

شعبة الخطابة الحسينية النسوية تنظّم مسابقة فرقية لطالبات برنامج ثمار العطاء

قسم العلاقات ينظم ورشة عن فن الإقناع والتواصل الفعّال للطلبة المنسقين

المزيد

الآخبار الصحية

تغيير بسيط في نمط التفكير قد يحدث فرقا كبيرا لصحة الدماغ ؟

لماذا ينعشنا المشروب الساخن في الطقس الحار؟

علماء يكتشفون فئة دم فريدة من نوعها في العالم !

لماذا ينصح الأطباء بزيت الزيتون يوميا؟

المزيد

الآخبار التكنلوجية

حساس الإطارات.. ما هو وعلامات تلفه وكيفية صيانته؟

ما معنى أودي Quattro؟ سر الأداء والتميز الهندسي ؟!

فصل الشاحن أم الهاتف أولا؟.. عادات بسيطة تطيل عمر البطارية

تعود للقرن الرابع قبل الميلاد.. اكتشاف بقايا "إيمت" المصرية

المزيد