تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Quintic Equation
المؤلف:
Chowla, S
المصدر:
"On Quintic Equations Soluble by Radicals." Math. Student 13
الجزء والصفحة:
...
17-2-2019
4400
Quintic Equation
Unlike quadratic, cubic, and quartic polynomials, the general quintic cannot be solved algebraically in terms of a finite number of additions, subtractions, multiplications, divisions, and root extractions, as rigorously demonstrated by Abel (Abel's impossibility theorem) and Galois. However, certain classes of quintic equations can be solved in this manner.
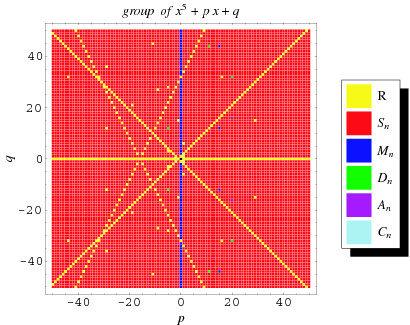
Irreducible quintic equations can be associated with a Galois group, which may be a symmetric group 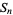 , metacyclic group
, metacyclic group 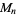 , dihedral group
, dihedral group 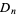 , alternating group
, alternating group 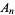 , or cyclic group
, or cyclic group 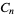 , as illustrated above. Solvability of a quintic is then predicated by its corresponding group being a solvable group. An example of a quintic equation with solvable cyclic group is
, as illustrated above. Solvability of a quintic is then predicated by its corresponding group being a solvable group. An example of a quintic equation with solvable cyclic group is
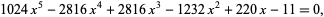 |
(1) |
which arises in the computation of 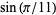 .
.
In the case of a solvable quintic, the roots can be found using the formulas found in 1771 by Malfatti, who was the first to "solve" the quintic using a resolvent of sixth degree (Pierpont 1895).
The general quintic can be solved in terms of Jacobi theta functions, as was first done by Hermite in 1858. Kronecker subsequently obtained the same solution more simply, and Brioschi also derived the equation. To do so, reduce the general quintic
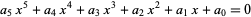 |
(2) |
into Bring quintic form
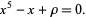 |
(3) |
Defining
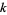 |
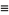 |
![tan[1/4sin^(-1)((16)/(25sqrt(5)rho^2))]](http://mathworld.wolfram.com/images/equations/QuinticEquation/Inline9.gif) |
(4) |
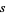 |
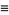 |
(5) |
|
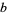 |
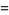 |
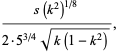 |
(6) |
where 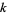 is the elliptic modulus, the roots of the original quintic are then given by
is the elliptic modulus, the roots of the original quintic are then given by
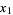 |
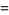 |
(7) |
|
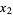 |
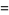 |
(8) |
|
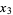 |
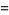 |
(9) |
|
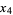 |
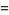 |
(10) |
|
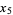 |
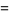 |
(11) |
where
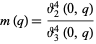 |
(12) |
is the inverse nome, which is expressible as a ratio of Jacobi theta functions.
Euler reduced the general quintic to
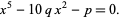 |
(13) |
A quintic also can be algebraically reduced to principal quintic form
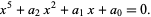 |
(14) |
By solving a quartic, a quintic can be algebraically reduced to the Bring quintic form, as was first done by Jerrard. Runge (1885) and Cadenhad and Young found a parameterization of solvable quintics in the form
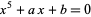 |
(15) |
by showing that all irreducible solvable quintics with coefficients of 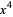 ,
, 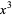 , and
, and 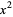 missing have the following form
missing have the following form
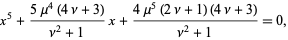 |
(16) |
where 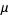 and
and  are rational.
are rational.
Spearman and Williams (1994) showed that an irreducible quintic of the form (15) having rational coefficients is solvable by radicals iff there exist rational numbers 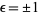 ,
, 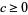 , and
, and 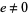 such that
such that
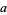 |
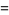 |
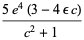 |
(17) |
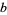 |
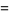 |
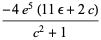 |
(18) |
(Spearman and Williams 1994). The roots are then
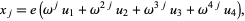 |
(19) |
where
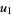 |
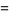 |
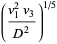 |
(20) |
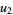 |
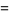 |
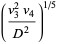 |
(21) |
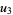 |
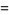 |
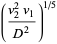 |
(22) |
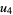 |
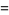 |
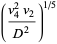 |
(23) |
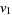 |
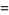 |
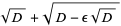 |
(24) |
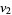 |
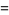 |
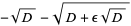 |
(25) |
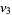 |
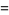 |
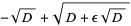 |
(26) |
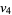 |
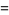 |
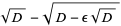 |
(27) |
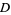 |
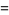 |
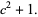 |
(28) |
Felix Klein used a Tschirnhausen transformation to reduce the general quintic to the form
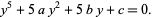 |
(29) |
He then solved the related icosahedral equation
![I(z,1,Z)=z^5(-1+11z^5+z^(10))^5
-[1+z^(30)-10005(z^(10)+z^(20))+522(-z^5+z^(25))]^2Z=0,](http://mathworld.wolfram.com/images/equations/QuinticEquation/NumberedEquation11.gif) |
(30) |
where 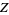 is a function of radicals of
is a function of radicals of 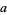 ,
, 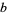 , and
, and 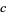 . The solution of this equation can be given in terms of hypergeometric functions as
. The solution of this equation can be given in terms of hypergeometric functions as
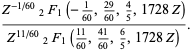 |
(31) |
Another possible approach uses a series expansion, which gives one root (the first one in the list below) of the Bring quintic form. All five roots can be derived using differential equations (Cockle 1860, Harley 1862). Let
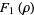 |
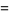 |
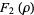 |
(32) |
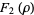 |
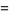 |
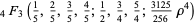 |
(33) |
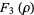 |
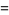 |
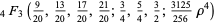 |
(34) |
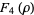 |
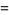 |
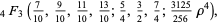 |
(35) |
 |
(36) |
then the roots are
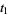 |
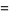 |
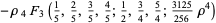 |
(37) |
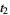 |
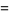 |
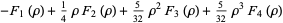 |
(38) |
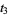 |
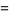 |
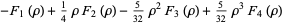 |
(39) |
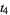 |
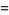 |
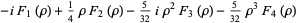 |
(40) |
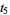 |
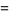 |
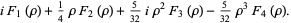 |
(41) |
This technique gives closed form solutions in terms of hypergeometric functions in one variable for any polynomialequation which can be written in the form
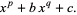 |
(42) |
Consider the quintic
![product_(j=0)^4[x-(omega^ju_1+omega^(4j)u_2)]=0,](http://mathworld.wolfram.com/images/equations/QuinticEquation/NumberedEquation14.gif) |
(43) |
where 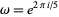 and
and 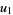 and
and 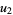 are complex numbers, which is related to de Moivre's quintic (Spearman and Williams 1994), and generalize it to
are complex numbers, which is related to de Moivre's quintic (Spearman and Williams 1994), and generalize it to
![product_(j=0)^4[x-(omega^ju_1+omega^(2j)u_2+omega^(3j)u_3+omega^(4j)u_4)]=0.](http://mathworld.wolfram.com/images/equations/QuinticEquation/NumberedEquation15.gif) |
(44) |
Expanding,
![(omega^ju_1+omega^(2j)u_2+omega^(3j)u_3+omega^(4j)u_4)^5-5U(omega^ju_1+omega^(2j)u_2+omega^(3j)u_3+omega^(4j)u_4)^3-5V(omega^ju_1+omega^(2j)u_2+omega^(3j)u_3+omega^(4j)u_4)^2+5W(omega^ju_1+omega^(2j)u_2+omega^(3j)u_3+omega^(4j)u_4)+[5(X-Y)-Z]=0,](http://mathworld.wolfram.com/images/equations/QuinticEquation/NumberedEquation16.gif) |
(45) |
where
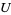 |
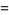 |
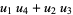 |
(46) |
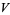 |
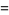 |
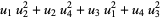 |
(47) |
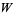 |
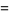 |
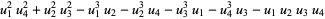 |
(48) |
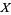 |
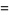 |
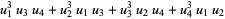 |
(49) |
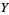 |
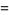 |
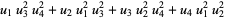 |
(50) |
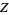 |
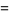 |
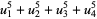 |
(51) |
(Spearman and Williams 1994). The 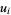 s satisfy
s satisfy
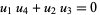 |
(52) |
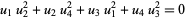 |
(53) |
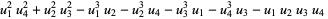 |
(54) |
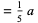 |
(55) |
![5[(u_1^3u_3u_4+u_2^3u_1u_3+u_3^3u_3u_4+u_4^3u_1u_2)-(u_1u_3^2u_4^2+u_2u_1^2u_3^2+u_3u_2^2u_4^2+u_4u_1^2u_2^2)]-(u_1^5+u_2^5+u_3^5+u_4^5)=b](http://mathworld.wolfram.com/images/equations/QuinticEquation/Inline131.gif) |
(56) |
(Spearman and Williams 1994).
REFERENCES:
Birkhoff, G. and Mac Lane, S. "Insolvability of Quintic Equations." §15.8 in A Survey of Modern Algebra, 5th ed. New York: Macmillan, pp. 418-421, 1996.
Chowla, S. "On Quintic Equations Soluble by Radicals." Math. Student 13, 84, 1945.
Cockle, J. "Sketch of a Theory of Transcendental Roots." Phil. Mag. 20, 145-148, 1860.
Cockle, J. "On Transcendental and Algebraic Solution--Supplemental Paper." Phil. Mag. 13, 135-139, 1862.
Davis, H. T. Introduction to Nonlinear Differential and Integral Equations. New York: Dover, p. 172, 1960.
Drociuk, R. J. "On the Complete Solution to the Most General Fifth Degree Polynomial." 3 May 2000. http://arxiv.org/abs/math.GM/0005026.
Dummit, D. S. "Solving Solvable Quintics." Math. Comput. 57, 387-401, 1991.
Glashan, J. C. "Notes on the Quintic." Amer. J. Math. 8, 178-179, 1885.
Green, M. L. "On the Analytic Solution of the Equation of Fifth Degree." Compos. Math. 37, 233-241, 1978.
Harley, R. "On the Solution of the Transcendental Solution of Algebraic Equations." Quart. J. Pure Appl. Math. 5, 337-361, 1862.
Harley, R. "A Contribution to the History of the Problem of the Reduction of the General Equation of the Fifth Degree to a Trinomial Form." Quart. J. Math. 6, 38-47, 1864.
Hermite, C. "Sulla risoluzione delle equazioni del quinto grado." Annali di math. pura ed appl. 1, 256-259, 1858.
King, R. B. Beyond the Quartic Equation. Boston, MA: Birkhäuser, 1996.
King, R. B. and Cranfield, E. R. "An Algorithm for Calculating the Roots of a General Quintic Equation from Its Coefficients." J. Math. Phys. 32, 823-825, 1991.
Klein, F. "Sull' equazioni dell' Icosaedro nella risoluzione delle equazioni del quinto grado [per funzioni ellittiche]." Reale Istituto Lombardo, Rendiconto, Ser. 2 10, 1877.
Klein, F. "Über die Transformation der elliptischen Funktionen und die Auflösung der Gleichungen fünften Grades." Math. Ann.14, 111-144, 1879.
Klein, F. Lectures on the Icosahedron and the Solution of Equations of the Fifth Degree. New York: Dover, 1956.
Livio, M. The Equation That Couldn't Be Solved. New York: Simon & Schuster, 2006.
Pierpont, J. "Zur Entwicklung der Gleichung V. Grades (bis 1858)." Monatsh. für Math. und Physik 6, 15-68, 1895.
Rosen, M. I. "Niels Hendrik Abel and Equations of the Fifth Degree." Amer. Math. Monthly 102, 495-505, 1995.
Runge, C. "Ueber die aufloesbaren Gleichungen von der Form 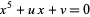 ." Acta Math. 7, 173-186, 1885.
." Acta Math. 7, 173-186, 1885.
Shurman, J. Geometry of the Quintic. New York: Wiley, 1997.
Spearman, B. K. and Williams, K. S. "Characterization of Solvable Quintics 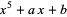 ." Amer. Math. Monthly 101, 986-992, 1994.
." Amer. Math. Monthly 101, 986-992, 1994.
Trott, M. "Solution of Quintics with Hypergeometric Functions." §3.13 in The Mathematica GuideBook for Symbolics. New York:Springer-Verlag, pp. 1110-1124, 2006. http://www.mathematicaguidebooks.org/.
Trott, M. and Adamchik, V. "Solving the Quintic with Mathematica." http://library.wolfram.com/infocenter/TechNotes/158/.
Wolfram Research. "Solving the Quintic." Poster. Champaign, IL: Wolfram Research, 1995. https://store.wolfram.com/view/misc/popup/solving-tqp.html.
Young, G. P. "Solution of Solvable Irreducible Quintic Equations, Without the Aid of a Resolvent Sextic." Amer. J. Math. 7, 170-177, 1885.
 الاكثر قراءة في مواضيع عامة في الجبر
الاكثر قراءة في مواضيع عامة في الجبر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)