تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Gröbner Basis
المؤلف:
Adams, W. W. and Loustaunau, P
المصدر:
An Introduction to Gröbner Bases. Providence, RI: Amer. Math. Soc., 1994.
الجزء والصفحة:
...
19-1-2019
2592
Gröbner Basis
A Gröbner basis 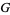 for a system of polynomials
for a system of polynomials 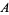 is an equivalence system that possesses useful properties, for example, that another polynomial
is an equivalence system that possesses useful properties, for example, that another polynomial 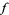 is a combination of those in
is a combination of those in 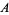 iff the remainder of
iff the remainder of 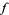 with respect to
with respect to 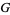 is 0. (Here, the division algorithm requires an order of a certain type on the monomials.) Furthermore, the set of polynomials in a Gröbner basis have the same collection of roots as the original polynomials. For linear functions in any number of variables, a Gröbner basis is equivalent to Gaussian elimination.
is 0. (Here, the division algorithm requires an order of a certain type on the monomials.) Furthermore, the set of polynomials in a Gröbner basis have the same collection of roots as the original polynomials. For linear functions in any number of variables, a Gröbner basis is equivalent to Gaussian elimination.
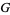 for a system of polynomials
for a system of polynomials 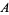 is an equivalence system that possesses useful properties, for example, that another polynomial
is an equivalence system that possesses useful properties, for example, that another polynomial 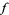 is a combination of those in
is a combination of those in 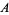 iff the remainder of
iff the remainder of 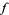 with respect to
with respect to 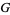 is 0. (Here, the division algorithm requires an order of a certain type on the monomials.) Furthermore, the set of polynomials in a Gröbner basis have the same collection of roots as the original polynomials. For linear functions in any number of variables, a Gröbner basis is equivalent to Gaussian elimination.
is 0. (Here, the division algorithm requires an order of a certain type on the monomials.) Furthermore, the set of polynomials in a Gröbner basis have the same collection of roots as the original polynomials. For linear functions in any number of variables, a Gröbner basis is equivalent to Gaussian elimination.
The algorithm for computing Gröbner bases is known as Buchberger's algorithm. Calculating a Gröbner basis is typically a very time-consuming process for large polynomial systems (Trott 2006, p. 37).
Gröbner bases are pervasive in the construction of symbolic algebra algorithms, and Gröbner bases with respect to lexicographic order are very useful for solving equations and for elimination of variables. For example, the following Wolfram Language command solves for the onset of the period-4 bifurcation in parameter 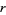 the logistic map by eliminating the variables
the logistic map by eliminating the variables 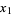 ,
, 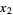 ,
, 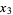 , and
, and 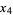 from a set of five equations describing the system.
from a set of five equations describing the system.
Factor /@ GroebnerBasis[
{
x2 - r x1(1 - x1),
x3 - r x2(1 - x2),
x4 - r x3(1 - x3),
x1 - r x4(1 - x4),
r^4(1 - 2x1)(1 - 2x2)(1 - 2x3)(1 - 2x4) + 1
},
r,
{x1, x2, x3, x4},
MonomialOrder -> EliminationOrder
]
Because computing a Gröbner basis can be so computationally expensive, variables can sometimes be eliminated more readily from a system of equations by manually computing the resultant of successive pairs of equations to iteratively eliminate one variable at each step.
The determination of a Gröbner basis is very roughly analogous to computing an orthonormal basis from a set of basisvectors and can be described roughly as a combination of Gaussian elimination (for linear systems) and the Euclidean algorithm (for univariate polynomials over a field).
The time and memory required to calculate a Gröbner basis depend very much on the variable ordering, monomialordering, and on which variables are regarded as constants. Gröbner bases are used implicitly in many routines in the Wolfram Language, and can be called explicitly with the command GroebnerBasis[{" src="http://mathworld.wolfram.com/images/equations/GroebnerBasis/Inline12.gif" style="height:14px; width:5px" />poly1, poly2, ...
}" src="http://mathworld.wolfram.com/images/equations/GroebnerBasis/Inline13.gif" style="height:14px; width:5px" />,
{" src="http://mathworld.wolfram.com/images/equations/GroebnerBasis/Inline14.gif" style="height:14px; width:5px" />x1, x2, ...
}" src="http://mathworld.wolfram.com/images/equations/GroebnerBasis/Inline15.gif" style="height:14px; width:5px" />].
In the common case of computing a Gröbner basis to eliminate trigonometric functions from a system of equations, the Weierstrass substitution
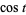 |
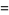 |
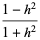 |
(1) |
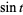 |
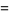 |
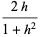 |
(2) |
where 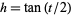 can be (but are not always) preferable to using
can be (but are not always) preferable to using 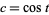 and
and 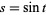 with the additional equation
with the additional equation 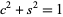 because they reduce the number of variables (Trott 2006, p. 39).
because they reduce the number of variables (Trott 2006, p. 39).
A bibliography about Gröbner bases is maintained by Buchberger and Zapletal.
In the Season 4 opening episode "Trust Metric" (2007) of the television crime drama NUMB3RS, math genius Charlie Eppes mentions that he used Gröbner bases in an attempt to derive an equation describing friendship.
REFERENCES:
Adams, W. W. and Loustaunau, P. An Introduction to Gröbner Bases. Providence, RI: Amer. Math. Soc., 1994.
Becker, T. and Weispfenning, V. Gröbner Bases: A Computational Approach to Commutative Algebra. New York: Springer-Verlag, 1993.
Boege, W.; Gebauer, R.; and Kredel, H. "Some Examples for Solving Systems of Algebraic Equations by Calculating Gröbner Bases." J. Symb. Comput. 1, 83-98, 1986.
Buchberger, B. "Gröbner Bases: An Algorithmic Method in Polynomial Ideal Theory." Ch. 6 in Multidimensional Systems Theory(Ed. N. K. Bose). New York: van Nostrand Reinhold, 1982.
Buchberger, B. "A Criterion for Detecting Unnecessary Reductions in the Construction of Groebner Bases." Proceedings of the International Symposium on Symbolic and Algebraic Computation. pp. 3-21, June 1979.
Buchberger, B. "Groebner Bases: A Short Introduction for Systems Theorists." http://www.risc.uni-linz.ac.at/people/buchberg/papers/2001-02-19-A.pdf.
Buchberger, B. and Zapletal, A. "Gröbner Bases Bibliography." http://www.ricam.oeaw.ac.at/Groebner-Bases-Bibliography/.
Cox, D.; Little, J.; and O'Shea, D. Ideals, Varieties, and Algorithms: An Introduction to Algebraic Geometry and Commutative Algebra, 2nd ed. New York: Springer-Verlag, 1996.
Eisenbud, D. Commutative Algebra with a View toward Algebraic Geometry. New York: Springer-Verlag, 1995.
Faugere, J. C.; Gianni, P.; Lazard, D.; and Mora, T. "Efficient Computation of Zero-Dimensional Groebner Bases by Change of Ordering." J. Symb. Comput. 16, 329-344, 1993.
Giovini, A.; Mora, T.; Niesi, G.; Robbiano, L.; and Traverso, C. "One Sugar Cube, Please?, or Selection Strategies in the Buchberger Algorithm." Proceedings of the International Symposium on Symbolic and Algebraic Computation. pp. 49-54, June 1991.
Harris, J. "Rearranging Expressions by Patterns." Mathematica J. 4, 82-85, 1994.
Heck, A. "A Bird's-Eye View of Gröbner Bases." http://www.can.nl/ca_library/groebner/tutorials/heck/aihenp96.html.
Helzer, G. "Gröbner Bases." Mathematica J. 5, 67-73, 1995.
Nakos, G. and Glinos, M. "Computing Gröbner Bases over the Integers." Mathematica J. 4, 70-75, 1994.
Lichtblau, D. "Gröbner Bases in Mathematica 3.0." Mathematica J. 6, 81-88, 1996.
McGettrick, M. "Buchberger Algorithm--Gröbner Basis--Sparse Multivariate Polynomials." http://grobner.nuigalway.ie/grobner/basis.html.
Mishra, B. Algorithmic Algebra. New York: Springer-Verlag, 1993.
Robbiano, L. "Term Ordering on the Polynomial Ring." In EUROCAL '85: European Conference on Computer Algebra, 1985 Linz, Austria, Vol. 2: Research Contributions New York: Springer-Verlag, 1986.
Stoutemyer, D. "Which Polynomial Representation is Best? Surprises Abound!" In Proceedings of the Third MACSYMA Users' Conference, Schenectady, NY. pp. 221-243, 1984.
Trott, M. "Applying GroebnerBasis to Three Problems in Geometry." Mathematica Educ. Res. 6, 15-28, 1997.
Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, pp. 32-50, 2006. http://www.mathematicaguidebooks.org/.
Wang, D. Elimination Methods. Berlin: Springer-Verlag, 1999.
 الاكثر قراءة في مواضيع عامة في الجبر
الاكثر قراءة في مواضيع عامة في الجبر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)