Relativistic Calculations
المؤلف:
E. R. Huggins
المصدر:
Physics 2000
الجزء والصفحة:
74
19-11-2020
1817
Relativistic Calculations
Although we have not quite finished with our discussion of Einstein’s special theory of relativity, we have covered two of the important consequences, time dilation and the Lorentz contraction, which will play important roles throughout the text. At this point we will take a short break to discuss easy ways to handle calculations involving these relativistic effects. Then we will take another look at Einstein’s theory to see if there are any more new effects to be discovered.
After our discussion of time dilation, we pointed out the importance of the quantity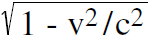 
which is a number always less than 1. If we wanted to know how much longer a moving observer’s time interval was, we divided by 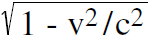to get a bigger number. If we wanted to know how much less was the frequency of a moving clock, we multiplied by 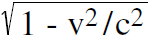to get a smaller number.
With the Lorentz contraction we have another effect that depends upon 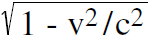. If we see an object go by us, the object will contract in length. To predict its contracted length, we multiply the uncontracted length by 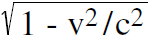to get a smaller number. If, on the other hand, an object moving by us had a contracted length l, and we stop the object, the contraction is undone and the length increases. We get the bigger uncontracted length by dividing by .
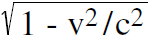As we mentioned earlier, first determine intuitively whether the number gets bigger or smaller, then either multiply by or divide by the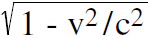 
as appropriate. This always works for time dilation, the Lorentz contraction, and, as we shall see later, relativistic mass. We will now work some examples involving the Lorentz contraction to become familiar with how to handle this effect.
الاكثر قراءة في النظرية النسبية الخاصة
اخر الاخبار
اخبار العتبة العباسية المقدسة
