Large Sample z Test
المؤلف:
D. A. Skoog, F. J.Holler, D M. West, and S. R. Crouch
المصدر:
Fundamentals of Analytical Chemistry
الجزء والصفحة:
9th. p 130
7-5-2017
2325
Large Sample z Test
If a large number of results are available so that s is a good estimate of s, the z test is appropriate. The procedure that is used is summarized below:
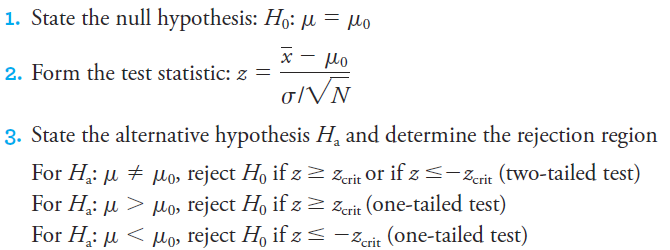
The rejection regions are illustrated in Figure 7-2 for the 95% confidence level.
Note that for Ha: μ ≠ μ0, we can reject for either a positive value of z or for a negative value of z that exceeds the critical value. This is called a two-tailed test since rejection can occur for results in either tail of the distribution. For the 95% confidence level, the probability that z exceeds zcrit is 0.025 in each tail or 0.05 total. Hence, there is only a 5% probability that random error will lead to a value of z ≥ -zcrit or z ≤ -zcrit. The significance level overall is α = 0.05. From Table 7-1, the critical value of z is 1.96 for this case. If instead our alternative hypothesis is Ha: μ > μ0, the test is said to be a onetailed test. In this case, we can reject only when z ≥ zcrit. Now, for the 95% confidence level, we want the probability that z exceeds zcrit to be 5% or the total
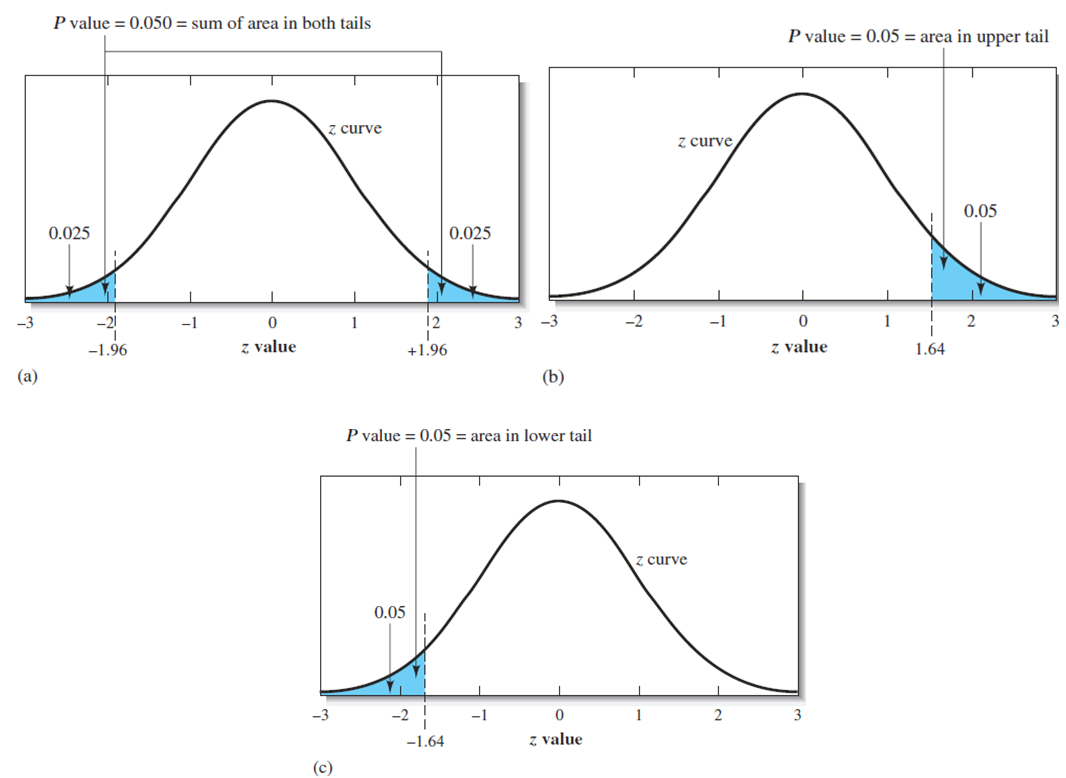
Figure 7-2 Rejection regions for the 95% confidence level. (a) Two-tailed test for Ha: μ ≠ μ0. Note the critical value of z is 1.96 . (b) One-tailed test for Ha: m > m0. The critical value of z is 1.64 so that 95% of the area is to the left of zcrit and 5% of the area is to the right. (c) One-tailed test for Ha: μ < μ0. The critical value is again 1.64 so that 5% of the area lies to the left of -zcrit.
الاكثر قراءة في مواضيع عامة في الكيمياء التحليلية
اخر الاخبار
اخبار العتبة العباسية المقدسة
