We know that if a great many forces are acting on a complicated mass of particles, whether the particles comprise a rigid or a nonrigid body, or a cloud of stars, or anything else, and we find the sum of all the forces (that is, of course, the external forces, because the internal forces balance out), then if we consider the body as a whole, and say it has a total mass M, there is a certain point “inside” the body, called the center of mass, such that the net resulting external force produces an acceleration of this point, just as though the whole mass were concentrated there. Let us now discuss the center of mass in a little more detail.
The location of the center of mass (abbreviated CM) is given by the equation

This is, of course, a vector equation which is really three equations, one for each of the three directions. We shall consider only the x-direction, because if we can understand that one, we can understand the other two. What does XCM=∑mixi/∑mi mean? Suppose for a moment that the object is divided into little pieces, all of which have the same mass m; then the total mass is simply the number N of pieces times the mass of one piece, say one gram, or any unit. Then this equation simply says that we add all the x’s, and then divide by the number of things that we have added: XCM= m∑xi/mN= ∑xi/N. In other words, XCM is the average of all the x’s, if the masses are equal. But suppose one of them were twice as heavy as the others. Then in the sum, that x would come in twice. This is easy to understand, for we can think of this double mass as being split into two equal ones, just like the others; then in taking the average, of course, we have to count that x twice because there are two masses there. Thus, X is the average position, in the x-direction, of all the masses, every mass being counted a number of times proportional to the mass, as though it were divided into “little grams.” From this it is easy to prove that X must be somewhere between the largest and the smallest x, and, therefore lies inside the envelope including the entire body. It does not have to be in the material of the body, for the body could be a circle, like a hoop, and the center of mass is in the center of the hoop, not in the hoop itself.
Of course, if an object is symmetrical in some way, for instance, a rectangle, so that it has a plane of symmetry, the center of mass lies somewhere on the plane of symmetry. In the case of a rectangle there are two planes, and that locates it uniquely. But if it is just any symmetrical object, then the center of gravity lies somewhere on the axis of symmetry, because in those circumstances there are as many positive as negative x’s.
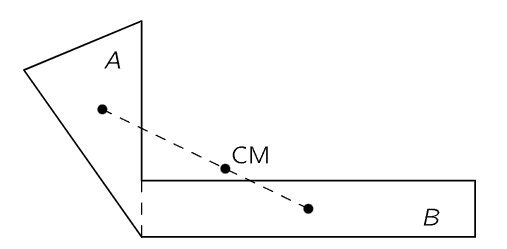
Fig. 19–1. The CM of a compound body lies on the line joining the CM’s of the two composite parts.
Another interesting proposition is the following very curious one. Suppose that we imagine an object to be made of two pieces, A and B (Fig. 19–1). Then the center of mass of the whole object can be calculated as follows. First, find the center of mass of piece A, and then of piece B. Also, find the total mass of each piece, MA and MB. Then consider a new problem, in which a point mass MA is at the center of mass of object A, and another point mass MB is at the center of mass of object B. The center of mass of these two point masses is then the center of mass of the whole object. In other words, if the centers of mass of various parts of an object have been worked out, we do not have to start all over again to find the center of mass of the whole object; we just have to put the pieces together, treating each one as a point mass situated at the center of mass of that piece. Let us see why that is. Suppose that we wanted to calculate the center of mass of a complete object, some of whose particles are considered to be members of object A and some members of object B. The total sum ∑mixi can then be split into two pieces—the sum ∑Amixi for the A object only, and the sum ∑Bmixi for object B only. Now if we were computing the center of mass of object A alone, we would have exactly the first of these sums, and we know that this by itself is MAXA, the total mass of all the particles in A times the position of the center of mass of A, because that is the theorem of the center of mass, applied to object A. In the same manner, just by looking at object B, we get MBXB, and of course, adding the two yields MXCM:
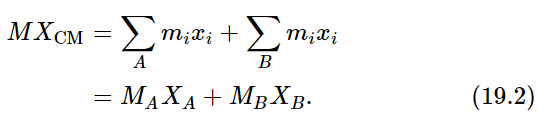
Now since M is evidently the sum of MA and MB, we see that Eq. (19.2) can be interpreted as a special example of the center of mass formula for two point objects, one of mass MA located at XA and the other of mass MB located at XB.
The theorem concerning the motion of the center of mass is very interesting, and has played an important part in the development of our understanding of physics. Suppose we assume that Newton’s law is right for the small component parts of a much larger object. Then this theorem shows that Newton’s law is also correct for the larger object, even if we do not study the details of the object, but only the total force acting on it and its mass. In other words, Newton’s law has the peculiar property that if it is right on a certain small scale, then it will be right on a larger scale. If we do not consider a baseball as a tremendously complex thing, made of myriads of interacting particles, but study only the motion of the center of mass and the external forces on the ball, we find F=ma, where F is the external force on the baseball, m is its mass, and a is the acceleration of its center of mass. So, F=ma is a law which reproduces itself on a larger scale. (There ought to be a good word, out of the Greek, perhaps, to describe a law which reproduces the same law on a larger scale.)
Of course, one might suspect that the first laws that would be discovered by human beings would be those that would reproduce themselves on a larger scale. Why? Because the actual scale of the fundamental gears and wheels of the universe are of atomic dimensions, which are so much finer than our observations that we are nowhere near that scale in our ordinary observations. So the first things that we would discover must be true for objects of no special size relative to an atomic scale. If the laws for small particles did not reproduce themselves on a larger scale, we would not discover those laws very easily. What about the reverse problem? Must the laws on a small scale be the same as those on a larger scale? Of course it is not necessarily so in nature, that at an atomic level the laws have to be the same as on a large scale. Suppose that the true laws of motion of atoms were given by some strange equation which does not have the property that when we go to a larger scale we reproduce the same law, but instead has the property that if we go to a larger scale, we can approximate it by a certain expression such that, if we extend that expression up and up, it keeps reproducing itself on a larger and larger scale. That is possible, and in fact that is the way it works. Newton’s laws are the “tail end” of the atomic laws, extrapolated to a very large size. The actual laws of motion of particles on a fine scale are very peculiar, but if we take large numbers of them and compound them, they approximate, but only approximate, Newton’s laws. Newton’s laws then permit us to go on to a higher and higher scale, and it still seems to be the same law. In fact, it becomes more and more accurate as the scale gets larger and larger. This self-reproducing factor of Newton’s laws is thus really not a fundamental feature of nature, but is an important historical feature. We would never discover the fundamental laws of the atomic particles at first observation because the first observations are much too crude. In fact, it turns out that the fundamental atomic laws, which we call quantum mechanics, are quite different from Newton’s laws, and are difficult to understand because all our direct experiences are with large-scale objects and the small-scale atoms behave like nothing we see on a large scale. So we cannot say, “An atom is just like a planet going around the sun,” or anything like that. It is like nothing we are familiar with because there is nothing like it. As we apply quantum mechanics to larger and larger things, the laws about the behavior of many atoms together do not reproduce themselves, but produce new laws, which are Newton’s laws, which then continue to reproduce themselves from, say, micro-microgram size, which still is billions and billions of atoms, on up to the size of the earth, and above.
Let us now return to the center of mass. The center of mass is sometimes called the center of gravity, for the reason that, in many cases, gravity may be considered uniform. Let us suppose that we have small enough dimensions that the gravitational force is not only proportional to the mass, but is everywhere parallel to some fixed line. Then consider an object in which there are gravitational forces on each of its constituent masses. Let mi be the mass of one part. Then the gravitational force on that part is mi times g. Now the question is, where can we apply a single force to balance the gravitational force on the whole thing, so that the entire object, if it is a rigid body, will not turn? The answer is that this force must go through the center of mass, and we show this in the following way. In order that the body will not turn, the torque produced by all the forces must add up to zero, because if there is a torque, there is a change of angular momentum, and thus a rotation. So we must calculate the total of all the torques on all the particles, and see how much torque there is about any given axis; it should be zero if this axis is at the center of mass. Now, measuring x horizontally and y vertically, we know that the torques are the forces in the y-direction, times the lever arm x (that is to say, the force times the lever arm around which we want to measure the torque). Now the total torque is the sum
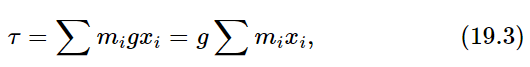
so, if the total torque is to be zero, the sum ∑mixi must be zero. But ∑mixi=MXCM, the total mass times the distance of the center of mass from the axis. Thus, the x-distance of the center of mass from the axis is zero.
Of course, we have checked the result only for the x-distance, but if we use the true center of mass the object will balance in any position, because if we turned it 90 degrees, we would have y’s instead of x’s. In other words, when an object is supported at its center of mass, there is no torque on it because of a parallel gravitational field. In case the object is so large that the nonparallelism of the gravitational forces is significant, then the center where one must apply the balancing force is not simple to describe, and it departs slightly from the center of mass. That is why one must distinguish between the center of mass and the center of gravity. The fact that an object supported exactly at the center of mass will balance in all positions has another interesting consequence. If, instead of gravitation, we have a pseudo force due to acceleration, we may use exactly the same mathematical procedure to find the position to support it so that there are no torques produced by the inertial force of acceleration. Suppose that the object is held in some manner inside a box, and that the box, and everything contained in it, is accelerating. We know that, from the point of view of someone at rest relative to this accelerating box, there will be an effective force due to inertia. That is, to make the object go along with the box, we have to push on it to accelerate it, and this force is “balanced” by the “force of inertia,” which is a pseudo force equal to the mass times the acceleration of the box. To the man in the box, this is the same situation as if the object were in a uniform gravitational field whose “g” value is equal to the acceleration a. Thus, the inertial force due to accelerating an object has no torque about the center of mass.
This fact has a very interesting consequence. In an inertial frame that is not accelerating, the torque is always equal to the rate of change of the angular momentum. However, about an axis through the center of mass of an object which is accelerating, it is still true that the torque is equal to the rate of change of the angular momentum. Even if the center of mass is accelerating, we may still choose one special axis, namely, one passing through the center of mass, such that it will still be true that the torque is equal to the rate of change of angular momentum around that axis. Thus, the theorem that torque equals the rate of change of angular momentum is true in two general cases: (1) a fixed axis in inertial space, (2) an axis through the center of mass, even though the object may be accelerating.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


