The Siegel theta function is a 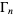-invariant meromorphic function on the space of all  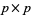symmetric complex matrices  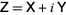with positive definite imaginary part. It is defined by

where 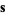 is a complex 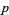-vector,  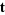is an integer 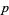-vector that ranges over the entire 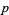-D lattice of integers, and  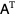denotes a matrix (or vector) transpose.

The Siegel theta function is implemented in the Wolfram Language as SiegelTheta[Omega, s].

This function was investigated by many of the luminaries of nineteenth century mathematics, Riemann, Weierstrass, Frobenius, Poincaré. Umemura has expressed the roots of an arbitrary polynomial in terms of Siegel theta functions (Mumford 1984).

REFERENCES:

Böcherer, S. and Schulze-Pillot, R. "Vector Valued Theta Series and Waldspurger's Theorem." Abh. Math. Sem. Univ. Hamburg 64, 211-233, 1994.

Borcherds, R. E. "Sporadic groups and string theory." In First European Congress of Mathematics. Vol. I. Invited lectures. Part 1. Proceedings of the congress held at the Sorbonne and Panthéon-Sorbonne Universities, Paris, July 6-10, 1992 Borcherds, R. E. "Automorphic Forms and Lie Algebras." In Current Developments in Mathematics, 1996. Papers from the Seminar Held in Cambridge, MA, 1996 (Ed. R. Bott, A. Jaffe, D. Jerison, G. Lusztig, I. Singer; and S. T. Yau). Boston, MA: International Press, pp. 1-36, 1997.

Borcherds, R. E. "Automorphic Forms with Singularities on Grassmannians." Invent. Math. 132, 491-562, 1998.

(Ed.  A. Joseph, F. Mignot, F. Murat, B. Prum, and R. Rentschler). Basel, Switzerland: Birkhäuser, pp. 411-421, 1994.

Iyanaga, S. and Kawada, Y. (Eds.). "Siegel Modular Functions." §34F in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 131-132, 1980.

Katok, S. and Sarnak, P. "Heegner Points, Cycles and Maass Forms." Israel J. Math. 84, 193-227, 1993.

Mumford, D. Part C in Tata Lectures on Theta. II. Jacobian Theta Functions and Differential Equations. Boston, MA: Birkhäuser, 1984.

Siegel, C. L. Topics in Complex Function Theory, Vol. 2: Automorphic Functions and Abelian Integrals. New York: Wiley, p. 163, 1988.

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد