Conservation of Energy
المؤلف:
Professor John W. Norbury
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
الجزء والصفحة:
p 98
15-12-2016
2342
Conservation of Energy
Let's summarize again. The work-energy theorem is ΔU + ΔK = WNC where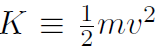 
and for gravity U = mgy. WNC is .the non-conservative work, such as friction, heat, sound, etc. It is often zero as in the next example
Example If you drop an object from a height H, with what speed does it hit the ground? Deduce the answer using the work energy theorem. Assume WNC = 0
Solution WNC = 0 because things such as heat and friction are negligible. Thus the work energy theorem is
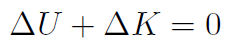
or
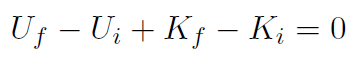
or
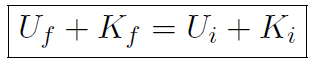
That is the total energy
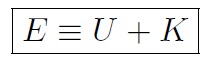
is constant. This is the famous conservation of mechanical energy,
i.e. Ef = Ei. We have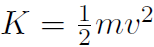 
and U = mgy giving
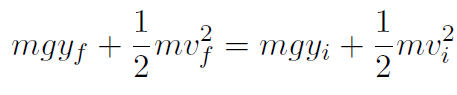
but yf = 0 and yi = H and vi = 0. Thus
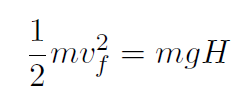
or
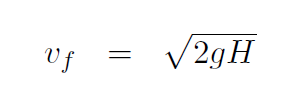
Example Complete the previous example using the constant acceleration equations
Solution The most convenient equation is
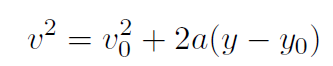
but v0 = 0 and y - y0 = 0- H = -H and a = -g, giving
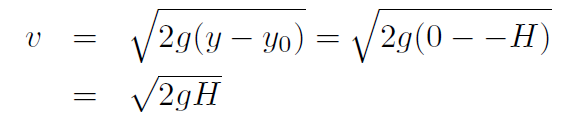
.which is the same answer as before
.(Example Prove that a swinging pendulum always rises to the same height. (Neglect friction
Solution With friction ignored we have WNC = 0 and
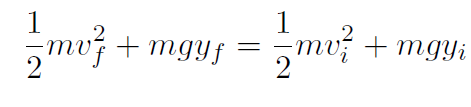
I let go of the pendulum with speed vi = 0 and it returns with speed vf = 0. Thus
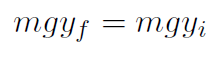
or
yf = yi
الاكثر قراءة في الميكانيك
اخر الاخبار
اخبار العتبة العباسية المقدسة
