Mixtures of gases
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
الجزء والصفحة:
ص12-14
2025-10-29
71
Mixtures of gases
When dealing with gaseous mixtures, we often need to know the contribution that each component makes to the total pressure of the sample. The partial pressure, pJ, of a gas J in a mixture (any gas, not just a perfect gas), is defined as pJ = xJp where xJ is the mole fraction of the component J, the amount of J expressed as a fraction of the total amount of molecules, n, in the sample:
When no J molecules are present, xJ = 0; when only J molecules are present, xJ = 1. It follows from the definition of xJ that, whatever the composition of the mixture, xA+xB+· · · =1 and therefore that the sum of the partial pressures is equal to the total pressure:
This relation is true for both real and perfect gases. When all the gases are perfect, the partial pressure as defined in eqn 1.13 is also the pressure that each gas would occupy if it occupied the same container alone at the same temperature. The latter is the original meaning of ‘partial pressure’. That identification was the basis of the original formulation of Dalton’s law:
The pressure exerted by a mixture of gases is the sum of the pressures that each one would exist if it occupied the container alone. Now, however, the relation between partial pressure (as defined in eqn 1.13) and total pressure (as given by eqn 1.15) is true for all gases and the identification of partial pressure with the pressure that the gas would exert on its own is valid only for a perfect gas.
Example 1.3 Calculating partial pressures
The mass percentage composition of dry air at sea level is approximately N2: 75.5; O2: 23.2; Ar: 1.3. What is the partial pressure of each component when the total pressure is 1.00 atm? Method We expect species with a high mole fraction to have a proportionally high partial pressure. Partial pressures are defined by eqn 1.13. To use the equation, we need the mole fractions of the components. To calculate mole fractions, which are defined by eqn 1.14, we use the fact that the amount of molecules J of molar mass MJ in a sample of mass mJ is nJ= mJ/MJ. The mole fractions are independent of the total mass of the sample, so we can choose the latter to be 100 g (which makes the conversion from mass percentages very easy). Thus, the mass of N2 present is 75.5 per cent of 100 g, which is 75.5 g. Answer The amounts of each type of molecule present in 100 g of air, in which the masses of N2, O2, and Ar are 75.5 g, 23.2 g, and 1.3 g, respectively, are
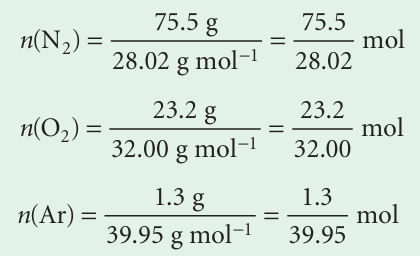
These three amounts work out as 2.69 mol, 0.725 mol, and 0.033 mol, respectively, for a total of 3.45 mol. The mole fractions are obtained by dividing each of the above amounts by 3.45 mol and the partial pressures are then obtained by multi plying the mole fraction by the total pressure (1.00 atm):
We have not had to assume that the gases are perfect: partial pressures are defined as pJ = xJp for any kind of gas.
Self-test 1.4 When carbon dioxide is taken into account, the mass percentages are 75.52 (N2), 23.15 (O2), 1.28 (Ar), and 0.046 (CO2). What are the partial pressures when the total pressure is 0.900 atm? [0.703, 0.189, 0.0084, 0.00027 atm]
الاكثر قراءة في مواضيع عامة في الكيمياء العضوية
اخر الاخبار
اخبار العتبة العباسية المقدسة
