يجري استخدام النسبية العامة في الحياة العادية في المسافات الفلكية الهائلة. وبالنسبة لمسافات بهذا الشكل فإن نظرية آينشتاين تعني أن غياب الكتلة معناه تسطح الفضاء كما يوضحالشكل رقم (3-3). 

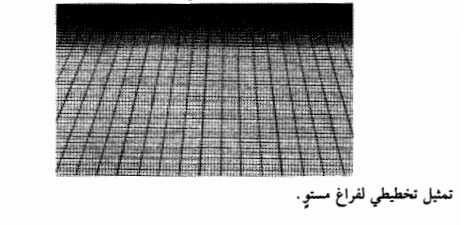الشكل رقم (3-3).

وللربط بين النسبية العامة وميكانيكا الكم لابد من أن نغير من بؤرة اهتمامنا بشكل حاد ونختبر الخواص المجهرية الميكروسكوبية للمكان. وقد أوضحنا ذلك في الشكل رقم (5-1)، وذلك بتقريب وتكبير مناطق صغيرة جداً في نسيج الفضاء. وعند بداية التقريب لن يحدث شيء كما نرى في المستويات الثلاثة الأولى للتكبير في الشكل رقم (5-1) حيث تحتفظ بنية الفضاء بشكلها الأساسي. ومن منطلق كلاسيكي بحث فإننا قد نتوقع أن الصورة الهادئة والمنبسطة للفضاء ستصمد حتى نصل إلى مقاييس صغيرة الطول. غير أن ميكانيكا الكم ستغير هذه النتيجة جذرياً. فكل شيء معرض للتأرجحات الكمية المتأصلة في مبدأ عدم التيقن - حتى مجال الجاذبية. وعلى الرغم من أن المنطق الكلاسيكي يتضمن أن الفضاء الخالي له مجال جاذبية مساو للصفر، فإن ميكانيكا الكم تبين أن قيمة المجال المتوسطة هي صفر لكن القيمة الفعلية تتأرجح لأعلى ولأسفل نتيجة التأرجح الكمي. والأكثر من ذلك، فإن مبدأ عدم التيقن ينبئنا بأن مدى التأرجح في مجال الجاذبية يزداد كلما زاد تركيز انتباهنا على مناطق أصغر في الفضاء المكان. وتوضح ميكانيكا الكم أنه لا شيء يفضل البقاء محصوراً في مكان ضيق، ويؤدي تضييق الفضاء إلى مزيد من ! التأرجحات. ولأن مجالات الجاذبية تظهر على شكل تحدب، فإن التأرجحات الكمية تظهر نفسها كتشوهات متزايدة العنف للفضاء للمكان المحيط. ونحن نرى بصيصاً هذه التشوهات يبزغ في المستوى الرابع للتكبير في الشكل رقم (5-1). و باختبار مستويات من المسافات الأقل كما يبين المستوى الخامس في الشكل رقم (5-1) فإننا نرى أن التأرجح العشوائي الكمي في مجال الجاذبية يقابله اعوجاج شديد في الفضاء بحيث لم يعد يمثل جسماً هندسياً ذا انحناءات رقيقة كما في حالة مثال الغشاء المطاطي الذي أوردناه في الفصل الثالث. وهو يتخذ بالأحرى شكلاً رغوياً هائجاً ملتوياً كما هو مبين بالجزء الأعلى من الشكل. وقد صك جون ويلر مصطلح الرغوة الكمية" ليصف الجنون الذي بينه الفحص فوق المجهري للمكان (وللزمان) - ويصف هذا مملكة غير مألوفة للكون حيث تفقد المفاهيم المتفق عليها لليسار واليمين وللأمام والخلف ولأعلى وأسفل بل وحتى مفهوم قبل وبعد) معناها وعلى مثل هذه المقاييس للمسافات الصغيرة فإننا نرى عدم التوافق الأساسي بين النسبية العامة وميكانيكا الكم وقد حطمت التأرجحات الكمية العنيفة التي تظهر عند مقاييس المسافات الصغيرة مفهوم الشكل الهندسي الفضائي الهادئ الذي هو المبدأ المحوري في النسبية العامة". وعلى المقاييس فوق المجهرية فإن السمة المحورية لميكانيكا الكم - مبدأ عدم التيقن - تتناقض السمة مباشرة مع المحورية للنسبية العامة - نموذج الفضاء المكان الهندسي الهادئ(والزمكان).

وعملياً يقحم هذا التناقض نفسه في كل أمر أساسي. فالحسابات التي تمزج بين معادلات النسبية العامة وميكانيكا الكم تؤدي بالضرورة إلى نفس الإجابة غير المنطقية: ما لا نهاية. وتشبه الإجابة بما لا نهاية أثراً حاداً تركه معلم من الطراز القديم لينبئنا بأننا نرتكب خطأ جسيم (6). ولا تستطيع معادلات النسبية العامة أن تتعامل مع الجنون الغاضب للرغوة الكمية. ومع . ذلك فإننا نلاحظ عندما نتراجع إلى مسافات أكثر اعتيادية (بالسير مع التتابع المرسوم في الشكل رقم (15) في الاتجاه العكسي)، أن التأرجحات العشوائية العنيفة الصغيرة تلاشي بعضها البعض - تماماً بنفس الطريقة التي لا يُظهر بها كشف الحساب البنكي لمدمن الاقتراض هذا الإدمان - ويصبح المفهوم الهندسي الهادئ لنسيج الكون مرة أخرى دقيقاً. ويشبه ذلك تماماً ما تراه عندما تنظر إلى صورة مركبة من شبكة من النقاط فإذا نظرت من بعيد فإن النقاط المكونة للصورة تمتزج بعضها مع بعض لتعطي الانطباع بصورة ناعمة تتغير فيها مناطق الإضاءة بهدوء وبلطف أما إذا فحصت الصورة عن قرب أكثر، فإن الأمر سيختلف بشكل ملحوظ عن تلك الصورة الناعمة التي تظهر عند النظر من مسافات بعيدة وليس الأمر سوى مجموعة من النقاط غير المترابطة كل منها منفصلة عن الأخرى. لكن لاحظ هنا أنك أدركت الطبيعة المنفصلة للصورة فقط عندما اختبرتها عن قرب، أما عن بعد فإنها تبدو ناعمة وبالمثل فإن نسيج الزمكان يبدو ناعماً إلا إذا اختبرناه بدقة فوق مجهرية. وهذا هو السبب في أن النسبية العامة تنطبق على مقاييس مسافات كبيرة بما فيه الكفاية (وأزمنة) - المقاييس المناسبة للكثير من الاستخدامات الفلكية العادية - لكنها تصبح غير متماشية عند مقاييس المسافات القصيرة (والأزمنة). وتصدق المقولة المحورية للتحدب الهندسي الرقيق الناعم على المقاييس الكبيرة، لكنها تتحطم نتيجة للتأرجحات الكمية عندما نطبقها على المقاييس الصغيرة.

الشكل رقم (5-1)

بالتكبير المتتابع | لمنطقة من الفضاء المكان يمكن فحص الخواص فوق المجهرية. وتصطدم محاولات مزج النسبية العامة وميكانيكا الكم بالرغوة الكمية العنيفة التي تبزغ عند أعلى مستوى للتكبير .

وتسمح لنا المبادئ الأساسية للنسبية العامة وميكانيكا الكم بحساب المقاييس التقريبية للمسافات التي علينا أن ننزل إلى أصغر منها لتظهر الظاهرة الغريبة الموجودة في الشكل رقم (5-1). ويتضافر كل من صغر ثابت بلانك – الذي يتحكم في شدة التأثيرات الكمية - والضعف الذاتي لقوى الجاذبية ليعطيا ما يعرف باسم "طول بلانك الذي من الصغر بحيث لا يمكن تخيله: فهو جزء من المليون من جزء من المليار من جزء من المليار من جزء من المليار من السنتيمتر

(^33-10سم). ويظهر المستوى الخامس في الشكل رقم (5-1) بشكل تخطيطي المستوى فوق المجهري عند مسافات أصغر من طول بلانك للكون. ولتقريب الإحساس بهذه المسافات فإننا إذا قمنا بتكبير ذرة واحدة إلى حجم مساو لحجم الكون المعروف لنا، فإن طول بلانك لن يتجاوز ارتفاع شجرة متوسطة.

وهكذا يصبح عدم التوافق بين النسبية العامة وميكانيكا الكم واضحاً فقط في جزء صغير من الكون مستوى محدود من (الكون. ولهذا السبب قد تتساءل عما إذا كان ذلك يستحق المعاناة؟ وفي الحقيقة فإن مجتمع الفيزياء لا يتخذ موقفاً موحداً عند تناول هذا الموضوع. فهناك فيزيائيون يعترفون بوجود المشكلة لكنهم يتجاوزونها ويستخدمون ميكانيكا الكم والنسبية العامة في تناول المشكلات التي تتعلق بالأطوال الأكبر كثيراً من طول ،بلانك، كما تتطلب ذلك أبحاثهم. إلا أنه هناك فيزيائيون آخرون لا يرتاحون تماماً لحقيقة التناقض الأساسي العميق بين الركيزتين الأساسيتين المعروفتين لنا في الفيزياء، بصرف النظر عن المسافات فوق المجهرية التي يجب اختبارها للكشف عن المشكلة. وهم يقولون إن عدم التطابق يشير إلى عيب أساسي في فهمنا للعالم الفيزيائي ويعتمد هذا الرأي على وجهة نظر غير مثبتة لكنها محسوسة بشدة بأن الكون إذا فهمناه على أعمق مستوياته وأكثرها أولية يمكن وصفه بواسطة نظرية تبدو منطقية متجانسة الأجزاء. وبالتأكيد، وبصرف النظر عن مدى محورية عدم التوافق هذا في أبحاثهم، فإن معظم الفيزيائيين يجدون من الصعب تصديق أن الفهم النظري للكون يتشكل من خليط متنافر رياضياً لإطارين قويين لكنهما متعارضان.

وقد قام الفيزيائيون بمحاولات عديدة لتنقيح النسبية العامة أو ميكانيكا الكم بشكل أو بآخر لتجنب هذا التناقض. وعلى الرغم من أن هذه المحاولات كانت جريئة وعبقرية إلا أنها باءت بالفشل الواحدة تلو الآخرى.

كان هذا سائداً حتى اكتشاف نظرية الأوتار الفائقة.

مواضيع ذات صلة

المكان والزمان وعين الراصد

هل هي موجة أم جسيمة؟

الحاجة إلى نظرية جديدة النسبية العامة في مواجهة ميكانيكا الكم

(التأثير في الزمن) تأثير الحركة على مرور الزمن: الساعة الضوئية وتباطؤ الزمن

الحركة خلال الزمكان (Spacetime)

تموجات في نسيج الزمكان: حين لحقت الجاذبية بالضوء (حل التناقض)

مرة أخرى اعوجاج الزمان(حين يتباطأ الزمن تحت ثقل الجاذبية)

التسارع واعوجاج المكان والزمان

عن الاعوجاجات والتموجات( في الزمكان )

أكثر أفكار آينشتاين إشراقاً

(الانشغال بالحياة) تأثير الحركة القريبة من سرعة الضوء على معدل انحلال الميونات وفق النسبية الخاصة

نظرية النسبية