تفاعل الجسيمات الثقيلة المشحونة مع المادة

عند تفاعل الجسيم الثقيل مع المادة فإنه لن يغير اتجاهه غالباً ولكنه يفقد جزء من طاقته إثر كل تصادم مع الإلكترونات. وسيكون معدل هذا الفقد صغيراً وبالتالي سيقوم هذا الجسيم بعدد كبير من التصادمات قبل أن يفقد كل طاقته ويمتص داخل المادة. وبالتالي يمكن معالجة التفاوت الناتج في فقد الطاقة إحصائياً ومن ثم يمكن أخذ قيمة متوسطة لهذا الفقد وهذا يعني أن هناك مدى محدد لهذه الجسيمات في المادة. يعرف معدل فقد الطاقة خلال مسير الجسيم بقوة الإيقاف (dE/dx-) التي يمكن حسابها: نظرياً باستخدام قوانين الميكانيكا الكلاسيكية كما فعل بوهر عام 1915 وبيث عام 1930 الذي عالج المشكلة باستخدام الميكانيكا الموجبة كما قام بلوخ Bloch عام 1933 باستنتاج علاقة دقيقة باستخدام ميكانيكا الكم. سوف نعالج المشكلة من وجهة نظر كلاسيكية كما يلي:

لنفترض أن لدينا جسيماً كتلته M وسرعته V وشحنته Ze سقط على الكترون مداري كتلته m وعلى بعد قدره (b) من مسار الجسيم. وذلك كما نبينه في الشكل (1). وسنفترض هنا ان سرعة الجسيم أقل كثيراً من سرعة

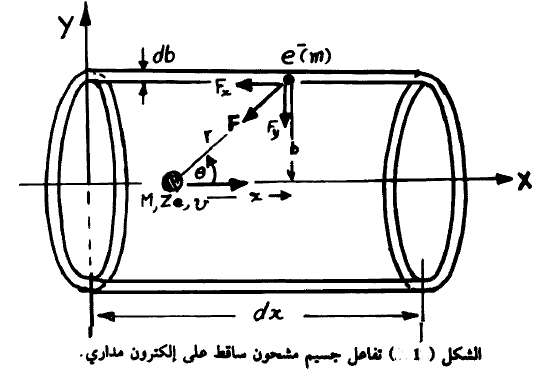
الضوء وبالتالي سنستخدم الميكانيكا الكلاسيكية في الحسابات. ويبدو أن ذلك صحيحاً بالنسبة للجسيمات الثقيلة ففي حالة جسيمات α فإن هذا التقريب صحيح إذا كانت طاقتها أقل من 10 م. أ. ف. وسنفترض أيضاً أن الإلكترون في مداره يعتبر ساكناً وأنه في مدار بعيد عن النواة وبالتالي سنعتبره حراً. وعلى هذا الأساس فإنه خلال التصادم بينه وبين الجسيم المشحون فلن يزاح عن موضعه. أو يتحرك مسافة قصيرة يمكن إهمالها بالنسبة لعامل التصادمImpact Parameter) b ) إن هذا التقريب يمكن أن يكون صحيحاً إذا كانت سرعة الجسيم المشحون عند تصادمه مع الإلكترون أكبر كثيراً من سرعة الإلكترون المداري. وبناءاً على ما سبق فإن الجسيم سيفقد طاقة عند تصادمه مع الإلكترون تساوي الطاقة التي سيكتسبها الإلكترون بعد التصادم. ويمكن حساب الأخيرة بمعرفة الزخم الذي سيكتسبه الإلكترون نتيجة لتصادم الجسيم المشحون معه.

تعطي القوة الكهربية بين الإلكترون والجسيم المشحون بالعلاقة:

(1) ...................

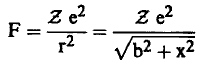
يمكن تحليل هذه القوة إلى مركبتين F_y في اتجاه عمودي على حركة الجسيم و F_x في اتجاه موازي لهذه الحركة. ومن التماثل الذي يبينه الشكل (1) فإن مركبة القوة المؤثرة على الإلكترون في الاتجاه الأخير تساوي صفراً. وتبقى فقط المركبة الرأسية F_y هي التي تؤثر على الإلكترون. وحيث أن الزخم P  يعطي بالعلاقة:

p = F dt

فإن:                ..........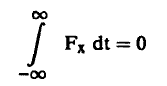

حيث    θF_x = F cos .

أما الزخم الرأسي P_y فيعطي بالعلاقة:

(2) .............

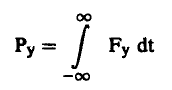
ولكن:  θ F_y = F sin

ومن ثم فإنه باستخدام المعادلة (1) نجد أن:

(3)................

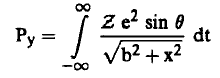
ومن الشكل (12. 2) نجد أن:

.....................

ونستطيع أيضاً التعويض عن dt بدلالة dx, v حيث:

وبالتعويض في معادلة (3) نجد أن:

(4)....................

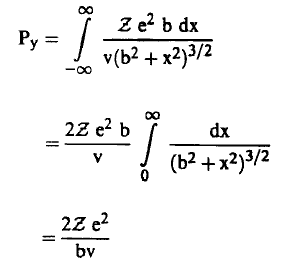
وبالتالي فإن الطاقة (E_e) التي سيكتسبها الإلكترون بعد التصادم (وتساوي نفس الطاقة التي يفقدها الجسيم) تعطي بالعلاقة :

(5)         ..........

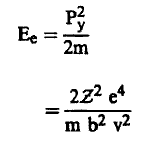
لنفترض الآن أن الجسيم تحرك مسافة dx في مادة تحوي N ذرة في وحدة الحجوم وكان العدد الذري لهذه المادة هو Z فإن عدد الإلكترونات في وحدة الحجوم يساري ZN. وسيكون عدد الإلكترونات في القشرة الأسطوانية التي يقع نصف قطرها بين  b, b + db وطولها dx يساوي dN.

(6)............. bdb . dx 2π. dN = NZ

وهذا العدد يمثل عدد التصادمات التي ستحدث بين الجسيم والإلكترونات. وبالتالي فإن الطاقة المفقودة بواسطة الجسيم والتي ستأخذها الإلكترونات في هذه القشرة هي dE حيث:

dE=Ee dN-

ومن معادلتي (5)، (6) نجد أن:

(7)..............

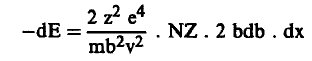
وبالتالي فإن الفقد الكلي للطاقة في وحدة الطول والذي ستكتسبه الإلكترونات في القشرة المحصورة بين b_max , b_min يعطي بالعلاقة:

(8)       ..............

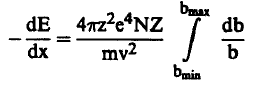
(9)       ..........

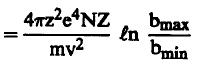
وهكذا لتعيين dE/dx ينبغي معرفة b_min, b_max . ويمكن حساب ذلك ببساطة وبالتقريب باستخدام الميكانيكا الكلاسيكية وذلك بحساب أقصى وأدنى طاقة يمكن أن يكتسبها الإلكترون نتيجة للتصادم:

أولاً: b_max: باستخدام معادلة (5) نجد أن الطاقة اللازمة لتأين الذرة هي I حيث:

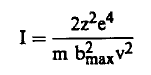
ومنها فإن:

(10)............

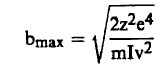
ثانياً : b_min : يمكن حساب هذه القيمة باعتبار أن أقصى سرعة يمكن ان يكتسبها الإلكترون في حالة التصادم المباشر Head - on cellisim عندما يساوي عامل التصادم (b_min) هي (2v). وبالتالي فإن طاقة حركته المكتسبة تساوي 1/2 mv² (كلاسيكياً) ومن ثم وباستخدام معادلة (5) نجد أن:

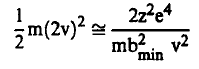
وبالتالي فإن:

(11)...........

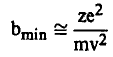
وبالتعويض من معادلتي (10)، (11) في معادلة (9) نجد أن:

(12)................

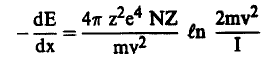
وفي حالة السرعات الكبيرة فإننا نستطيع أن ندخل الميكانيكا النسبية وبالتالي نحصل على العلاقة التالية:

(13) ..............

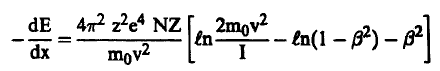
حيث: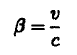   

m₀ هي كتلة السكون للإلكترون.

لاحظ أنه عندما تكون v صغيرة بالمقارنة مع C فإن معادلة (13) تؤول إلى الصورة الكلاسيكية (12). كما ويمكن كتابة dE/dx بدلالة كتلة (M) وطاقة الجسيم E حيث v² =2E/M  وبالتعويض عن قيمة v في معادلة (12) فإن:

(14)     ...........

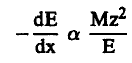
تبين هذه المعادلة أن معدل فقد الطاقة يزداد عندما تتباطأ الجسيمات الساقطة، وبالتالي فإن كثافة التأيين تزداد. وهذا ما بيناه في حالة جسيمات α. كما يزداد معدل الفقد بزيادة شحنة الجسيم الساقط. لاحظ أن قوة الإيقاف المعطاة بمعادلتي (12، 13) لن تكون صحيحة في حالة الجسيمات البطيئة. لقد وجد مثلاً أنها ليست صحيحة في حالة جسيمات α بطاقة قدرها أقل من 5 م.أ.ف. وكذلك بالنسبة للبروتونات التي تقل طاقتها عن 3. 1. م. أ. ف. ويرجع ذلك إلى أن الاختلاف بين الحسابات النظرية والقياسات العملية عند هذه الطاقات يرجع إلى أنه عند الطاقات المنخفضة فإن الجيمات تستطيع أن تلتقط الإلكترونات وتعود فتفقدها أثناء سيرها. وذلك لم يؤخذ في الحسبان عندما تم استنتاج العلاقتين المذكورتين أعلاه.

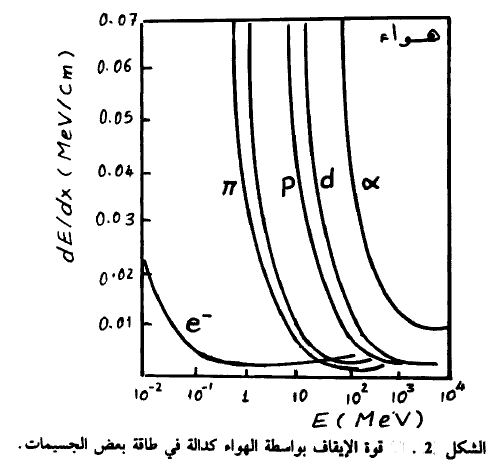
يبين الشكل (2) قوة الإيقاف بواسطة الهواء كدالة في طافة بعض الجسيمات.

لاحظ أنه يمكن حساب عدد الإيونات (i) في وحدة المسار التي يمكن أن تنتج عن الإشعاع من العلاقة:

(15)...........

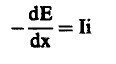
عملياً، يجب قياس I للمواد المختلفة، إلا أنه توجد علاقة مستنتجة عملياً حيث وجد أنه يمكن حساب I للعناصر الأثقل من الألمنيوم مقدرة بوحدة (أ. ف) حيث:

(16)                    .......

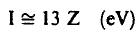حيث Z العدد الذري للعنصر،

مواضيع ذات صلة

أنواع أخرى من المفاعلات

تصاميم مفاعلات متقدمة

انواع المفاعلات النووية

اضطرابات السمت

لماذا طاقات أعلى؟

معجلات الطاقة الفائقة الإرتفاع

التطوير التاريخي للمعجلات

الحقل المغناطيسي وتأثيراته في البلازما والحقول الأخرى

انعطاف صغير عند النجوم

ما الحرارة في الاندماج النووي

التسخين بالحقن بذرات متعادلة

الاندماج النووي في المختبر