حل معادلة شرودنجر

بإهمال الحركة الانتقالية للجزيئة نبحث المعادلة الآتية:

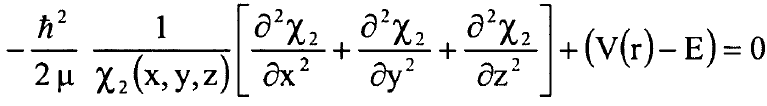..................(1)

حيث E تمثل طاقة الجزيئة الداخلية الدورانية والاهتزازية وفي ما يلي سنستبدل الدالة χ₂ بالدالة χ ومعلوم ان المقصود هو χ₂ ويمكن كتابة معادلة شرودنجر (1) بالصيغة:

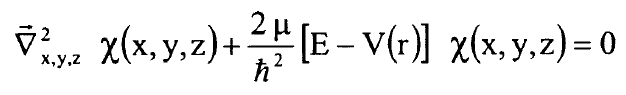......................(2)

ويمكن حل المعادلة (2) بالاحداثيات الكروية القطبية بفصل المتغيرات وكتابة الحل كحاصل ضرب ثلاث دوال:

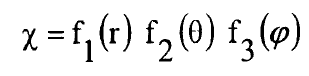..............(3)

بتعويض المعادلة (3) في المعادلة (2) نصل الى:

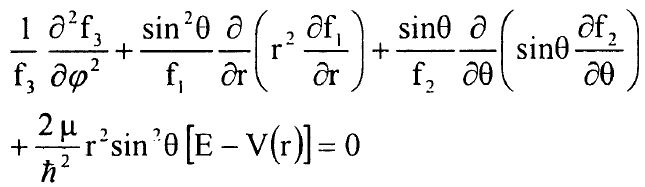....................(4)

حيث اصبحت المعادلة جمع حدود مستقلة وكل حد يحتوي متغير واحد فقط ولكي تكون ممكنة يجب ان يساوي كل حد مقدارا ثابتا ولذلك ناخذ الحد الاول مساويا الى الثالث α والحد الاخير مساويا الى α –  ويجب ان تصح هذه العلاقة: α = - m² حيث m عدد حقيقي وعندئذ يكون الحل للجزء الثالث بالشكل:

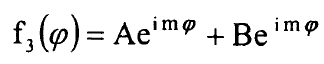
ولان الدالة الموجية يجب ان تكون احادية القيمة فيجب ان يكون لها نفس القيمة بعد اضافة π2 لذلك يجب ان ياخذ العدد m القيم الصحيحة التالية:

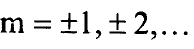
وبعد قسمة المعادلة (4) على sin²θ نحصل على التعبير:

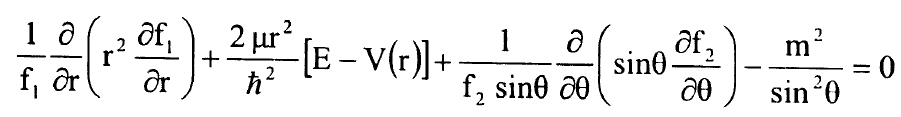..................(5)

ولكي تتحقق المعادلة (5) يجب ان تصح العلاقة:

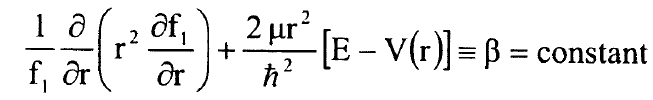...............(6)

وايضا تصح العلاقة:

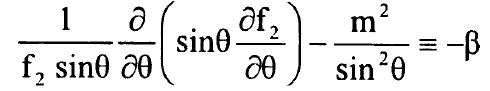................(7)

ان المعادلة (6) تحتوي المتغير r فقط والمعادلة (7) تضم المتغير r فقط ويمكن حل المعادلة (7) بواسطة المتوالية:

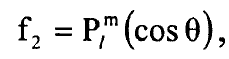
حيث / دليل المتوالية و (β= l (l +1 وm دليل وليس اس. ان الدوال P_l تدعى متعددة حدود ليجندر واذا وضعنا cos θ = u نصل الى:

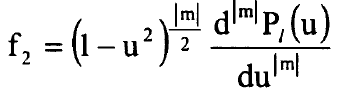
حيث:

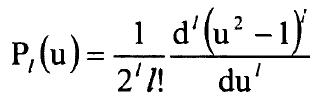
ويتحقق الشرط:

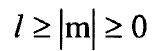
حيث / العدد الكمي للزخم الزاوي وتصبح الان المعادلة (6) بالشكل:

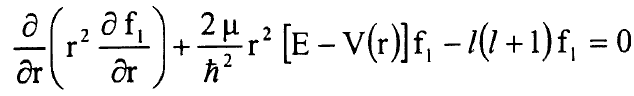....................(8)

ان المعادلة (8) هي المعادلة النصف قطرية والتي يمكن ايجاد حلها بعد معرفة الشكل الصريح للجهد (V(r ويمكن وضعها بالشكل:

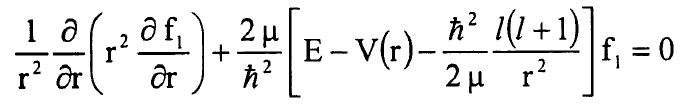....................(9)

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

الكشف عن الألغام والمتفجرات

الكربون .. أمير المواد وعميدها

خواص المواد النانوية

تاريخ أنابيب الكربون النانوية (History of carbon nanotubes)

الاتصال والحوار العام في تطوير تقنية النانو

نشاطات المنظمات الدولية في مجال التقنية النانوية

حالة المعارف المتصلة بمخاطر المواد النانوية

الاعتبارات الأخلاقية في التقنية النانويه

المنفعة الاجتماعية للتقنية النانوية

ما المقصود بالنانو؟

النانو تكنولوجيا.. علم وصناعة القرن الجديد

أنابيب الكربون النانوية Nanotubes Carbon