Prime Diophantine Equations
المؤلف:
Jones, J. P.; Sato, D.; Wada, H.; and Wiens, D.
المصدر:
"Diophantine Representation of the Set of Prime Numbers." Amer. Math. Monthly 83
الجزء والصفحة:
...
19-9-2020
1248
Prime Diophantine Equations
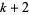is prime iff the 14 Diophantine equations in 26 variables
 |
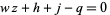(1)
|
 |
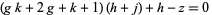(2)
|
 |
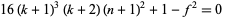(3)
|
 |
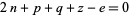(4)
|
 |
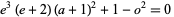(5)
|
 |
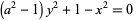(6)
|
 |
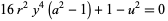(7)
|
 |
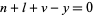(8)
|
 |
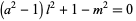(9)
|
 |
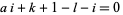(10)
|
![<span style=]() {[a+u^2(u^2-a)]^2-1}(n+4dy)^2+1-(x+cu)^2=0 " src="https://mathworld.wolfram.com/images/equations/PrimeDiophantineEquations/Inline12.gif" style="height:22px; width:312px" /> |
(11)
|
 |
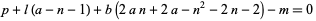(12)
|
 |
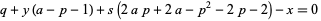(13)
|
 |
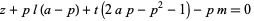(14)
|
have a solution in positive integers (Jones et al. 1976; Riesel 1994, p. 40).
REFERENCES:
Jones, J. P.; Sato, D.; Wada, H.; and Wiens, D. "Diophantine Representation of the Set of Prime Numbers." Amer. Math. Monthly 83, 449-464, 1976.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, 1994.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
