Morgan-Voyce Polynomials
المؤلف:
Swamy, M. N. S.
المصدر:
"Properties of the Polynomials Defined by Morgan-Voyce." Fib. Quart. 4
الجزء والصفحة:
...
20-9-2019
2005
Morgan-Voyce Polynomials
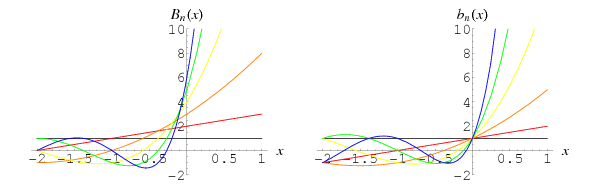
The Morgan-Voyce polynomials are polynomials related to the Brahmagupta and Fibonacci polynomials. They are defined by the recurrence relations
for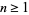 
, with
 |
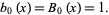(3)
|
Alternative recurrences are
with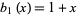 
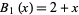and 
, and
The polynomials can be given explicitly by the sums
Defining the matrix
![Q=[x+2 -1; 1 0]](http://mathworld.wolfram.com/images/equations/Morgan-VoycePolynomials/NumberedEquation2.gif) |
(10)
|
gives the identities
Defining
gives
and
The Morgan-Voyce polynomials are related to the Fibonacci polynomials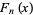 
by
(Swamy 1968ab).
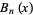satisfies the ordinary differential equation
 |
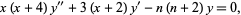(21)
|
and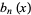 
the equation
 |
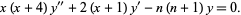(22)
|
These and several other identities involving derivatives and integrals of the polynomials are given by Swamy (1968).
REFERENCES:
Lahr, J. "Fibonacci and Lucas Numbers and the Morgan-Voyce Polynomials in Ladder Networks and in Electric Line Theory." In Fibonacci Numbers and Their Applications (Ed. G. E. Bergum, A. N. Philippou, and A. F. Horadam). Dordrecht, Netherlands: Reidel, 1986.
Morgan-Voyce, A. M. "Ladder Network Analysis Using Fibonacci Numbers." IRE Trans. Circuit Th. CT-6, 321-322, Sep. 1959.
Swamy, M. N. S. "Properties of the Polynomials Defined by Morgan-Voyce." Fib. Quart. 4, 73-81, 1966a.
Swamy, M. N. S. "More Fibonacci Identities." Fib. Quart. 4, 369-372, 1966b.
Swamy, M. N. S. "Further Properties of Morgan-Voyce Polynomials." Fib. Quart. 6, 167-175, 1968.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
