Thomae,s Theorem
المؤلف:
Bailey, W. N.
المصدر:
Generalised Hypergeometric Series. Cambridge, England: University Press, 1935.
الجزء والصفحة:
...
23-5-2019
2093
Thomae's Theorem
Thomae's theorem, also called Thomae's transformation, is the generalized hypergeometric function identity
 |
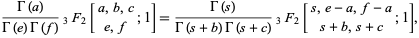(1)
|
where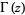 
is the gamma function, 
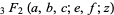is a generalized hypergeometric function,
 |
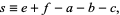(2)
|
and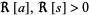 
(Bailey 1935, p. 14). It is a generalization of Dixon's theorem (Slater 1966, p. 52).
An equivalent formulation is given by
 |
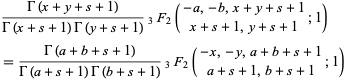(3)
|
(Hardy 1999, p. 104). The symmetry of this form was used by Ramanujan in his proof of the identity, which is essentially the same as Thomae's. Interestingly, this is one of the few cases in which Ramanujan gives an explicit proof of one of his propositions (Hardy 1999, p. 104).
A special case of the theorem is given by
 |
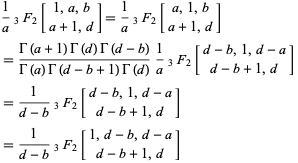(4)
|
(J. Sondow, pers. comm., May 25, 2003).
REFERENCES:
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: University Press, 1935.
Hardy, G. H. "A Chapter from Ramanujan's Note-Book." Proc. Cambridge Philos. Soc. 21, 492-503, 1923.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 104-105, 1999.
Slater, L. J. Generalized Hypergeometric Functions. Cambridge, England: Cambridge University Press, p. 52, 1966.
Thomae, J. "Ueber die Funktionen welche durch Reihen von der Form dargestellt werden: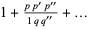 
." J. für Math. 87, 26-73, 1879.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
