We have seen that the imaginary part of the index means absorption. We shall now use this knowledge to find out how much energy is carried by a light wave. We have given earlier an argument that the energy carried by light is proportional to 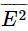, the time average of the square of the electric field in the wave. The decrease in E due to absorption must mean a loss of energy, which would go into some friction of the electrons and, we might guess, would end up as heat in the material.

If we consider the light arriving on a unit area, say one square centimeter, of our plate in Fig. 31–1, then we can write the following energy equation (if we assume that energy is conserved, as we do!):

Energy in per sec=

                        energy out per sec+work done per sec.                             (31.23)

For the first term we can write 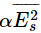, where α is the as yet unknown constant of proportionality which relates the average value of E² to the energy being carried. For the second term we must include the part from the radiating atoms of the material, so we should use 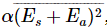, or (evaluating the square)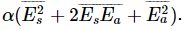

All of our calculations have been made for a thin layer of material whose index is not too far from 1, so that E_a would always be much less than E_s (just to make the calculations easier). In keeping with our approximations, we should, therefore, leave out the term 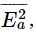, because it is much smaller than  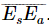You may say: “Then you should leave out  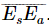also, because it is much smaller than 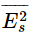.” It is true that  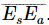is much smaller than 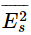, but we must keep  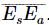or our approximation will be the one that would apply if we neglected the presence of the material completely! One way of checking that our calculations are consistent is to see that we always keep terms which are proportional to N Δz, the area density of atoms in the material, but we leave out terms which are proportional to (N Δz)² or any higher power of N Δz. Ours is what should be called a “low-density approximation.”

In the same spirit, we might remark that our energy equation has neglected the energy in the reflected wave. But that is OK because this term, too, is proportional to (N Δz)², since the amplitude of the reflected wave is proportional to N Δz.

For the last term in Eq. (31.23) we wish to compute the rate at which the incoming wave is doing work on the electrons. We know that work is force times distance, so the rate of doing work (also called power) is the force times the velocity. It is really F⋅v, but we do not need to worry about the dot product when the velocity and force are along the same direction as they are here (except for a possible minus sign). So, for each atom we take 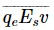for the average rate of doing work. Since there are N Δz atoms in a unit area, the last term in Eq. (31.23) should be  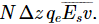Our energy equation now looks like

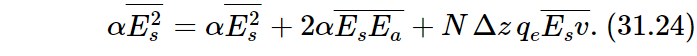
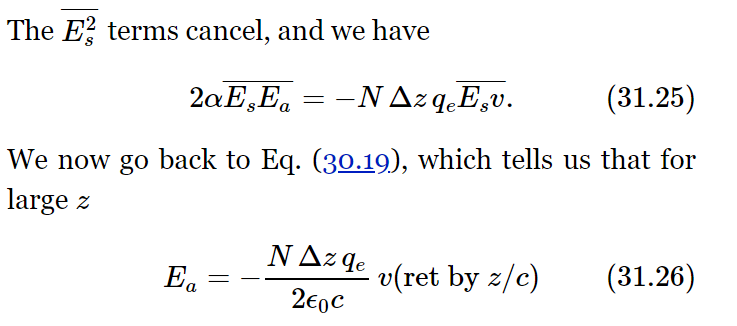
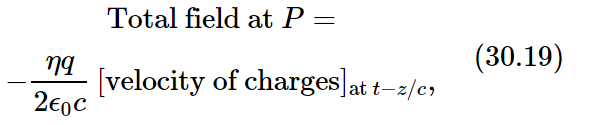
(recalling that η=N Δz). Putting Eq. (31.26) into the left-hand side of (31.25), we get

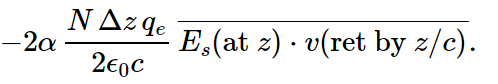
However, E_s (at z) is E_s (at atoms) retarded by z/c. Since the average is independent of time, it is the same now as retarded by z/c, or is 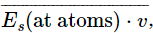 the same average that appears on the right-hand side of (31.25). The two sides are therefore equal if

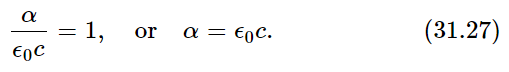
We have discovered that if energy is to be conserved, the energy carried in an electric wave per unit area and per unit time (or what we have called the intensity) must be given by 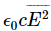. If we call the intensity 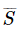, we have

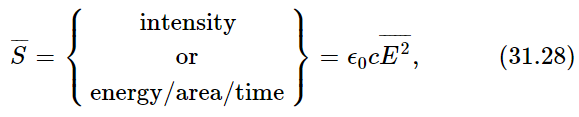
where the bar means the time average. We have a nice bonus result from our theory of the refractive index!