From his better understanding of the theory of motion, Newton appreciated that the sun could be the seat or organization of forces that govern the motion of the planets. Newton proved to himself (and perhaps we shall be able to prove it soon) that the very fact that equal areas are swept out in equal times is a precise sign post of the proposition that all deviations are precisely radial—that the law of areas is a direct consequence of the idea that all of the forces are directed exactly toward the sun.

Next, by analyzing Kepler’s third law it is possible to show that the farther away the planet, the weaker the forces. If two planets at different distances from the sun are compared, the analysis shows that the forces are inversely proportional to the squares of the respective distances. With the combination of the two laws, Newton concluded that there must be a force, inversely as the square of the distance, directed in a line between the two objects.

Being a man of considerable feeling for generalities, Newton supposed, of course, that this relationship applied more generally than just to the sun holding the planets. It was already known, for example, that the planet Jupiter had moons going around it as the moon of the earth goes around the earth, and Newton felt certain that each planet held its moons with a force. He already knew of the force holding us on the earth, so he proposed that this was a universal force—that everything pulls everything else.

The next problem was whether the pull of the earth on its people was the “same” as its pull on the moon, i.e., inversely as the square of the distance. If an object on the surface of the earth falls 16 feet in the first second after it is released from rest, how far does the moon fall in the same time? We might say that the moon does not fall at all. But if there were no force on the moon, it would go off in a straight line, whereas it goes in a circle instead, so it really falls in from where it would have been if there were no force at all. We can calculate from the radius of the moon’s orbit (which is about 240,000 miles) and how long it takes to go around the earth (approximately 29 days), how far the moon moves in its orbit in 1 second, and can then calculate how far it falls in one second. ² This distance turns out to be roughly 1/20 of an inch in a second. That fits very well with the inverse square law, because the earth’s radius is 4000 miles, and if something which is 4000 miles from the center of the earth falls 16 feet in a second, something 240,000 miles, or 60 times as far away, should fall only 1/3600 of 16 feet, which also is roughly 1/20 of an inch. Wishing to put this theory of gravitation to a test by similar calculations, Newton made his calculations very carefully and found a discrepancy so large that he regarded the theory as contradicted by facts, and did not publish his results. Six years later a new measurement of the size of the earth showed that the astronomers had been using an incorrect distance to the moon. When Newton heard of this, he made the calculation again, with the corrected figures, and obtained beautiful agreement.

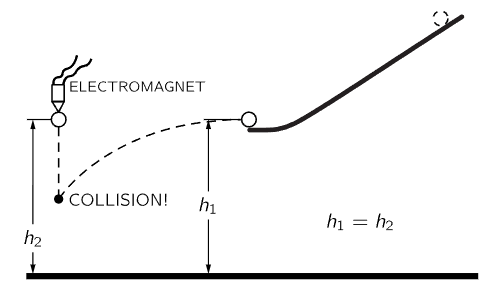
Fig. 7–3. Apparatus for showing the independence of vertical and horizontal motions.

This idea that the moon “falls” is somewhat confusing, because, as you see, it does not come any closer. The idea is sufficiently interesting to merit further explanation: the moon falls in the sense that it falls away from the straight line that it would pursue if there were no forces. Let us take an example on the surface of the earth. An object released near the earth’s surface will fall 16 feet in the first second. An object shot out horizontally will also fall 16 feet; even though it is moving horizontally, it still falls the same 16 feet in the same time. Figure 7–3 shows an apparatus which demonstrates this. On the horizontal track is a ball which is going to be driven forward a little distance away. At the same height is a ball which is going to fall vertically, and there is an electrical switch arranged so that at the moment the first ball leaves the track, the second ball is released. That they come to the same depth at the same time is witnessed by the fact that they collide in midair. An object like a bullet, shot horizontally, might go a long way in one second—perhaps 2000 feet—but it will still fall 16 feet if it is aimed horizontally. What happens if we shoot a bullet faster and faster? Do not forget that the earth’s surface is curved. If we shoot it fast enough, then when it falls 16 feet it may be at just the same height above the ground as it was before. How can that be? It still falls, but the earth curves away, so it falls “around” the earth. The question is, how far does it have to go in one second so that the earth is 16 feet below the horizon? In Fig. 7–4 we see the earth with its 4000-mile radius, and the tangential, straight-line path that the bullet would take if there were no force. Now, if we use one of those wonderful theorems in geometry, which says that our tangent is the mean proportional between the two parts of the diameter cut by an equal chord, we see that the horizontal distance travelled is the mean proportional between the 16 feet fallen and the 8000-mile diameter of the earth. The square root of (16/5280) × 8000 comes out very close to 5 miles. Thus, we see that if the bullet moves at 5 miles a second, it then will continue to fall toward the earth at the same rate of 16 feet each second, but will never get any closer because the earth keeps curving away from it. Thus, it was that Mr. Gagarin maintained himself in space while going 25,000 miles around the earth at approximately 5 miles per second. (He took a little longer because he was a little higher.)

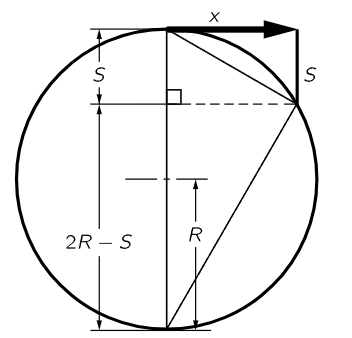
Fig. 7–4. Acceleration toward the center of a circular path. From plane geometry, x/S=(2R−S)/x≈2R/x, where R is the radius of the earth, 4000 miles; x is the distance “travelled horizontally” in one second; and S is the distance “fallen” in one second (16 feet).

Any great discovery of a new law is useful only if we can take more out than we put in. Now, Newton used the second and third of Kepler’s laws to deduce his law of gravitation. What did he predict? First, his analysis of the moon’s motion was a prediction because it connected the falling of objects on the earth’s surface with that of the moon. Second, the question is, is the orbit an ellipse? We shall see in a later chapter how it is possible to calculate the motion exactly, and indeed one can prove that it should be an ellipse,³ so no extra fact is needed to explain Kepler’s first law. Thus, Newton made his first powerful prediction.

The law of gravitation explains many phenomena not previously understood. For example, the pull of the moon on the earth causes the tides, hitherto mysterious. The moon pulls the water up under it and makes the tides—people had thought of that before, but they were not as clever as Newton, and so they thought there ought to be only one tide during the day. The reasoning was that the moon pulls the water up under it, making a high tide and a low tide, and since the earth spins underneath, that makes the tide at one station go up and down every 24 hours. Actually, the tide goes up and down in 12 hours. Another school of thought claimed that the high tide should be on the other side of the earth because, so they argued, the moon pulls the earth away from the water! Both of these theories are wrong. It actually works like this: the pull of the moon for the earth and for the water is “balanced” at the center. But the water which is closer to the moon is pulled more than the average and the water which is farther away from it is pulled less than the average. Furthermore, the water can flow while the more rigid earth cannot. The true picture is a combination of these two things.

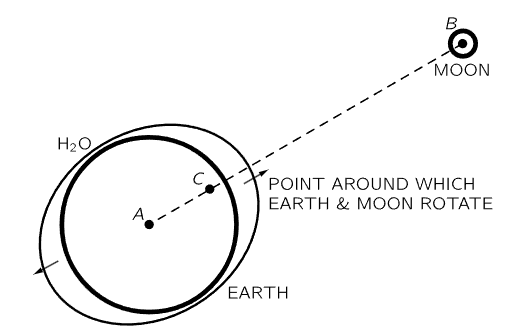
Fig. 7–5. The earth-moon system, with tides.

What do we mean by “balanced”? What balances? If the moon pulls the whole earth toward it, why doesn’t the earth fall right “up” to the moon? Because the earth does the same trick as the moon, it goes in a circle around a point which is inside the earth but not at its center. The moon does not just go around the earth, the earth and the moon both go around a central position, each falling toward this common position, as shown in Fig. 7–5. This motion around the common center is what balances the fall of each. So, the earth is not going in a straight line either; it travels in a circle. The water on the far side is “unbalanced” because the moon’s attraction there is weaker than it is at the center of the earth, where it just balances the “centrifugal force.” The result of this imbalance is that the water rises up, away from the center of the earth. On the near side, the attraction from the moon is stronger, and the imbalance is in the opposite direction in space, but again away from the center of the earth. The net result is that we get two tidal bulges.

____________________________________________________________________
Margin

2- That is, how far the circle of the moon’s orbit falls below the straight-line tangent to it at the point where the moon was one second before.

3- The proof is not given in this course.