
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-5-2018
Date: 9-9-2019
Date: 18-8-2018
|
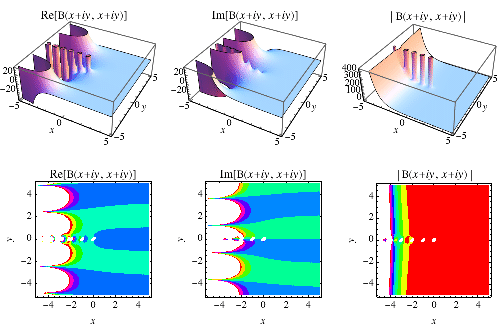 |
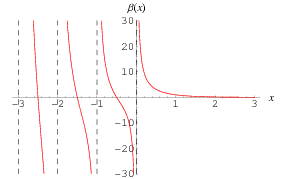
The central beta function is defined by
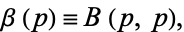 |
(1) |
where 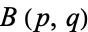 is the beta function. It satisfies the identities
is the beta function. It satisfies the identities
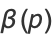 |
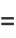 |
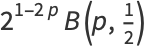 |
(2) |
 |
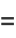 |
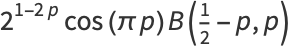 |
(3) |
 |
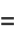 |
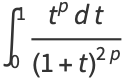 |
(4) |
 |
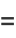 |
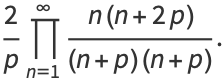 |
(5) |
With 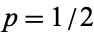 , the latter gives the Wallis formula. For
, the latter gives the Wallis formula. For 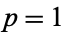 , 2, ... the first few values are 1, 1/6, 1/30, 1/140, 1/630, 1/2772, ... (OEIS A002457), which have denominators
, 2, ... the first few values are 1, 1/6, 1/30, 1/140, 1/630, 1/2772, ... (OEIS A002457), which have denominators 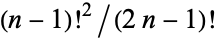 .
.
When 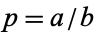 ,
,
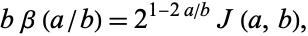 |
(6) |
where
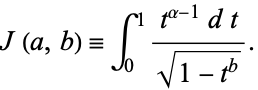 |
(7) |
The central beta function satisfies
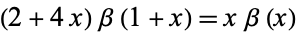 |
(8) |
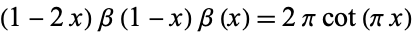 |
(9) |
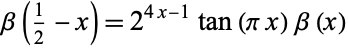 |
(10) |
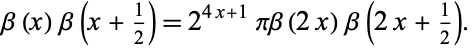 |
(11) |
For  an odd positive integer, the central beta function satisfies the identity
an odd positive integer, the central beta function satisfies the identity
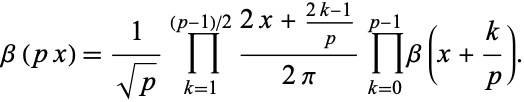 |
(12) |
REFERENCES:
Borwein, J. M. and Zucker, I. J. "Elliptic Integral Evaluation of the Gamma Function at Rational Values of Small Denominators." IMA J. Numerical Analysis 12, 519-526, 1992.
Sloane, N. J. A. Sequence A002457/M4198 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
هل يمكن للدماغ البشري التنبؤ بالمستقبل أثناء النوم؟
|
|
|
|
|
|
|
علماء: طول الأيام على الأرض يزداد بسبب النواة الداخلية
|
|
|
|
|
|
|
المجمع العلمي يشرك طلبة الدورات الصيفية بمحفلٍ قرآني في محافظة بابل
|
|
|