


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-8-2018
Date: 19-9-2018
Date: 25-8-2018
|
The quintuple product identity, also called the Watson quintuple product identity, states
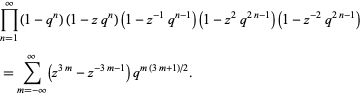 |
(1) |
It can also be written
![product_(n=1)^infty(1-q^(2n))(1-q^(2n-1)z)(1-q^(2n-1)z^(-1))(1-q^(4n-4)z^2)(1-q^(4n-4)z^(-2))
=sum_(n=-infty)^inftyq^(3n^2-2n)[(z^(3n)+z^(-3n))-(z^(3n-2)+z^(-(3n-2)))]](http://mathworld.wolfram.com/images/equations/QuintupleProductIdentity/NumberedEquation2.gif) |
(2) |
or
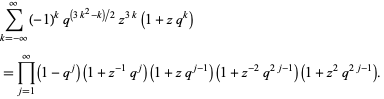 |
(3) |
The quintuple product identity can be written in q-series notation as
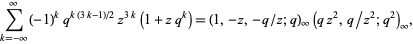 |
(4) |
where 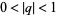 and
and 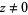 (Gasper and Rahman 1990, p. 134; Leininger and Milne 1999).
(Gasper and Rahman 1990, p. 134; Leininger and Milne 1999).
Using the notation of the Ramanujan theta function (Berndt 1985, p. 83),
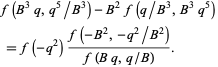 |
(5) |
REFERENCES:
Berndt, B. C. Ramanujan's Notebooks, Part III. New York:Springer-Verlag, 1985.
Bhargava, S. "A Simple Proof of the Quintuple Product Identity." J. Indian Math. Soc. 61, 226-228, 1995.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 306-309, 1987.
Carlitz, L. and Subbarao, M. V. "A Simple Proof of the Quintuple Product Identity." Proc. Amer. Math. Soc. 32, 42-44, 1972.
Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, 1990.
Leininger, V. E. and Milne, S. C. "Some New Infinite Families of 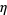 -Function Identities." Methods Appl. Anal. 6, 225-248, 1999b.
-Function Identities." Methods Appl. Anal. 6, 225-248, 1999b.
|
|
|
|
اكتشاف تأثير صحي مزدوج لتلوث الهواء على البالغين في منتصف العمر
|
|
|
|
|
|
|
زهور برية شائعة لتر ميم الأعصاب التالفة
|
|
|
|
|
|
العتبة العباسية تطلق مسابقة فن التصوير الفوتوغرافي الثانية للهواة ضمن فعاليات أسبوع الإمامة الدولي
|
|
|
|
لجنة البرامج المركزيّة تختتم فعاليّات الأسبوع الرابع من البرنامج المركزي لمنتسبي العتبة العباسيّة
|
|
|
|
قسم المعارف: عمل مستمر في تحقيق مجموعة من المخطوطات ستسهم بإثراء المكتبة الدينية
|
|
|
|
متحف الكفيل يشارك في المؤتمر الدولي الثالث لكلية الآثار بجامعة الكوفة
|