معادلة الانتشار Diffusion Equation

دعنا نحسب الآن معدل تسرب النيوترونات من حجم معين. يبين الشكل (1) عنصر حجم dV عبارة عن صندوق أبعاده dx dy dz موضوع عند النقطة (z, y, x) فيكون عدد النيوترونات الدي يخترق الوجه الأسفل للصندوق مساوياً J_z dxdy نيوترون/ث. ويكون عدد النيوترونات الذي يغادر الوجه المقابل لهذا الوجه أو الوجه العلوي مساوياً (J_z+dz dxdy ) لاحظ هنا أن J_z تعبر عن محصلة

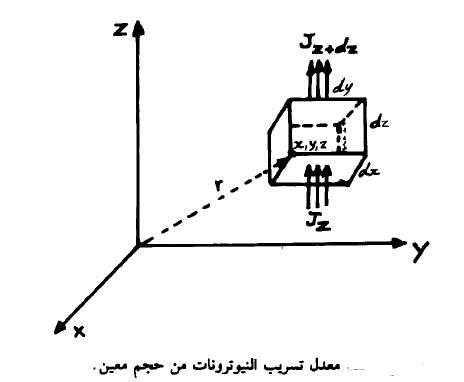
الشكل (1)

تيار النيوترونات في اتجاه Z.

معدل الإنتاج (production) - معدل الامتصاص (absorption) + معدل التسرب (Leakage).....(1)

ومن معادلة (1) وباستبدال D_o بالقيمة D وكذلك كثافة النيوترونات بالفيض ∅ وباعتبار أن D ثابتة فإن المحصلة النهائية لمعدل تدفق النيوتررنات من عنصر الحجم خلال الوجه الموازي للسطح xy تعطي بالعلاقة:

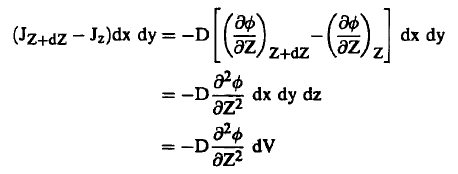
وبالمثل يمكن كتابة تعابير تعطي معدل تدفق النيوترونات من الوجهين الآخرين لعنصر الحجم، ففي اتجاه X نجد أن معدل التدفق يعطي بالقيمة :

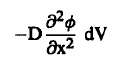
وفي اتجاه Y يعطي بالقيمة:

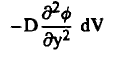
ويعطي معدل التسرب الكلي للنيوترونات من وحدة الحجوم dV بجمع الكميات الثلاث السابقة ويعطي معدل التسرب/ وحدة الحجوم بالقسمة على dV، ويتتج أن:

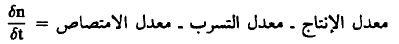........(2)

يمكننا الآن التعويض في معادلة (2) حيث نجد أن معدل الامتصاص يعطي بالقيمة ∅ _a∑ حيث _a∑ مساحة مقطع الامتصاص الماكروسكوبي للنيوترونات الحرارية. وبوضع معدل الإنتاج مساوياً للقيمة S حيث تسمى بحد المصدر Source Term وبالتالي ينتج أن معادلة (2) تأخذ الصورة التالية:

(3)...............

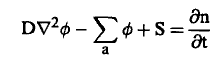
وتعرف هذه المعادلة بمعادلة الانتشار. وتعتبر صحيحة فقط في حالة النيوترونات وحيدة الطاقة. وسوف نطبقها على النيوترونات الحرارية المتحركة في وسط ضعيف الامتصاص للنيوترونات. في حالة لاستقرار نجد أن n/∂t∂ = صفر وينتج أن:

(4)...........

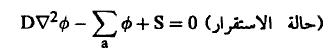
وفي حالة غياب مصدر النيوترونات فإن ٍS = صفر وينتج أن هذه المعادلة تؤول إلى العلاقة:

(5)..............

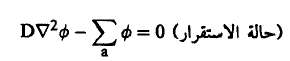
التي يمكن وضعها على الصورة:

(6).............

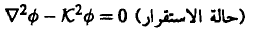
حيث:

(7)..........

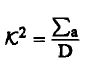
لاحظ هنا أن أبعاد _a∑ هي معكوس الطول أما D فتؤخذ بوحدات الطول. وينتج أن أبعاد K هي معكوس الطول. ومن ثم يمكن تعيين الكمية L التي تعرف بطول الانتشار Diffusion Length حيث:

(8)............

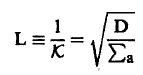
دعنا نحسب الآن انتشار النيوترونات وحيدة الطاقة من مصدر نقطي، ودعنا نفترض أن المصدر موضوع عند نقطة الأصل، ومن ثم فإن المصدر سيكون متماثلاً كروياً. ولإيجاد الفيض ∅ في معادلة (6) دعنا نضع هذا الفيض على الصورة:

(9).............

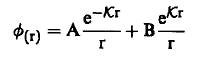
لاحظ أن هذه الصورة تحقق المعادلة (6). وبأخذ الشروط الابتدائية نجد أنه عندما تؤول (r) إلى ما لانهاية فإن الفيض يجب أن ينعدم ومن ثم تؤول (∅) إلى الصورة:

(10).............

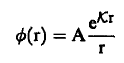
حيث r المسافة بين نقطة القياس والمصدر.

A ثابت، يمكن تعيينه كما يلي:

لنفترض أن قوة المصدر هي Q نيوترون/ث. في جميع الاتجاهات. وبافتراض أن هناك كرة نصف قطرها r وأن J هي تيار النيوترونات فيكون عدد النيوترونات التي تخترق سطح الكرة/ث مساوياً للمقدار 4πr² J ويكون نهاية هذا المقدار عندما r  → 0 هي Q ومن ثم فإن:

(11)..............

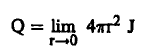
ومن معادلة الاتية:

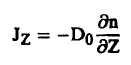
 نجد أن:

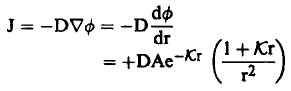
وبالتعويض في معادلة (11) نجد أن:

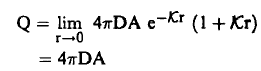
أي أن:

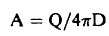
ومن ثم ينتج أن الفيض ∅ يعطي بالعلاقة:

(12) .............

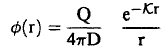
ويمكن إيجاد مفهوم طبيعي للقيمة κ وذلك بتقدير متوسط مربع المسافة r² بين مصدر النيوترونات والنقطة التي يمتص فيها النيوترون والتي تبعد مسافة قدرها r عنه حيث:

(13)    .................

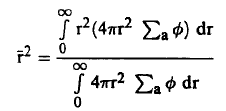
وبالتعويض عن ∅ من معادلة (12) نجد أن:

(14).........

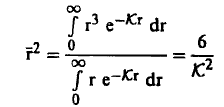
ومن معادلة (8) نجد أن:

(15)    .............

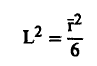
يبين الجدول (1) خصائص مهدئات معينة لنيوترونات معينة.

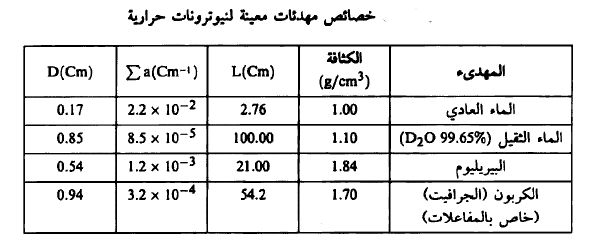
الجدول (1)

وحسب نظرية الانتشار فإنه يمكن إثبات أن طول الانتشار (L) يمكن أن يعطي بالعلاقة التالية وذلك عند استخدام منظومة منخفضة الامتصاص:

(16).............

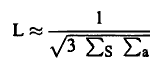
حيث _S, ∑_a∑ مساحتي مقطعي الامتصاص الماكروسكوبي والتشتت على الترتيب.

مواضيع ذات صلة

أنواع أخرى من المفاعلات

تصاميم مفاعلات متقدمة

انواع المفاعلات النووية

اضطرابات السمت

لماذا طاقات أعلى؟

معجلات الطاقة الفائقة الإرتفاع

التطوير التاريخي للمعجلات

الحقل المغناطيسي وتأثيراته في البلازما والحقول الأخرى

انعطاف صغير عند النجوم

ما الحرارة في الاندماج النووي

التسخين بالحقن بذرات متعادلة

الاندماج النووي في المختبر