طريقة المربعات الصغرى Least Square Method

تستخدم هذه الطريقة لرسم أفضل خط مستقيم يمر بمجموعة من النقاط (أو بعضها). لنفترض أن لدينا مجموعة من البيانات تمثل بعائلة من النقاط (كل منها لها إحداثيان y, x). أي أن هذه النقاط هي:

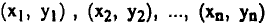
ونريد الآن رسم خط مستقيم يمر بكل أو بمعظم هذه النقاط .

تعطي معادلة الخط المستقيم بالعلاقة:

y = mx+c

حيث m ميل الخط.

C طول الجزء المقطوع من محور الصادات (y) .

لاحظ أنه لكل قيمة من قيم x المقاسة (_box) توجد قيمتان للمتغير لا. أحدهما هي قيمة y المقاسة (y_ob) والأخرى هي قيمة لا الواقعة على الخط المستقيم. وقد تختلف هاتان القيمتان عن بعضهما ونعبر عن الاختلاف بالرمز ى حيث.

(1)...........

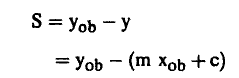ومن ثم نحصل على مجموعة من الاختلافات، أي أن:

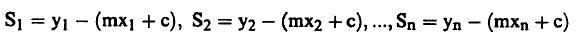
تعبر هذه المجموعة عن مدى انطباق الخط المستقيم مع القيم المقاسة. و نحصل على خط مستقيم يمر بالنقاط جميعاً عندما يساوي كل اختلاف صفراً.

دعنا نعرف الآن الدالة (c ,g(m حيث:

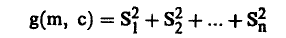
أي أن:

(2).............

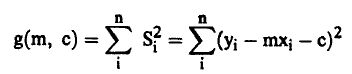
حسب مبدأ المربعات الصغرى فإن أفضل خط مستقيم يمر بالنقاط السابقة هو الخط الذي تبلغ عنده (g(m, c قيمة صفري أي أن:      

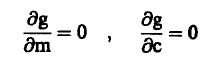
وبالتعويض من معادلة (2) نجد أن هذا الشرط يتحقق عندما:

(3).............

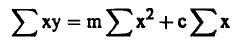
(4).............

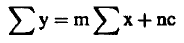
ويحل هاتين المعادلتين يمكن ايجاد قيمة كلا من المجهولين C, m. ومن ثم نحدد افضل خط مستقيم يمر بالنقاط العملية.

مواضيع ذات صلة

أنواع أخرى من المفاعلات

تصاميم مفاعلات متقدمة

انواع المفاعلات النووية

اضطرابات السمت

لماذا طاقات أعلى؟

معجلات الطاقة الفائقة الإرتفاع

التطوير التاريخي للمعجلات

الحقل المغناطيسي وتأثيراته في البلازما والحقول الأخرى

انعطاف صغير عند النجوم

ما الحرارة في الاندماج النووي

التسخين بالحقن بذرات متعادلة

الاندماج النووي في المختبر