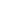معاملات التحول (α) Conversion Coefficients

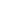
تعتبر معاملات التحول قيم ذات أهمية بالغة للفيزياء النووية. ويمكن تعريف معامل التحول على أنه النسبة بين ثابت انحلال التحول الداخلي. وثابت انحلال ( أي أن:

(1)............

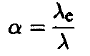
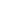
أي أنه النسبة بين معدل انطلاق الكترونات التحول الداخلي (أو عددها N_e) ومعدل انطلاق إشعاع γ (أو عدد الفوتونات _γN). أي أن:

(2)...........

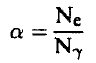
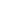
ويمكن تعيين α الخاص بمدار معين والناتج عن انطلاق الإلكترون من ذلك المدار. فمثلاً يمكن تعريف _Kα باعتباره معامل التحول الخاص بانطلاق الإلكترون من المدار K ومن ثم فإن:

(3)..................

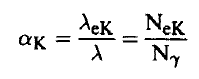
حيث N_eK هو عدد الإلكترونات المنطلقة من المدار K.

وبالمثل يمكن تعريف _m α_L، α ..... حيث:

وبالتالي فإن معامل التحول الكلي (معادلة 2) يمكن أن يأخذ الصورة:

(4)...........

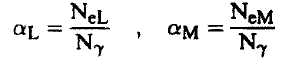
كما ويمكن لإلكترون المدار L أن يخرج من المدارات الفرعية L₁ ، L₂، ... وبالتالي تأخذ المعادلة السابقة الصورة:

(5)     ..............

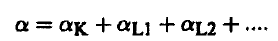
ومن ثم يمكن كتابة معادلة الاتية

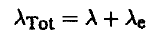
على الصورة:

(6)............

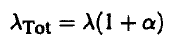
او

(7)     ...............

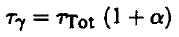
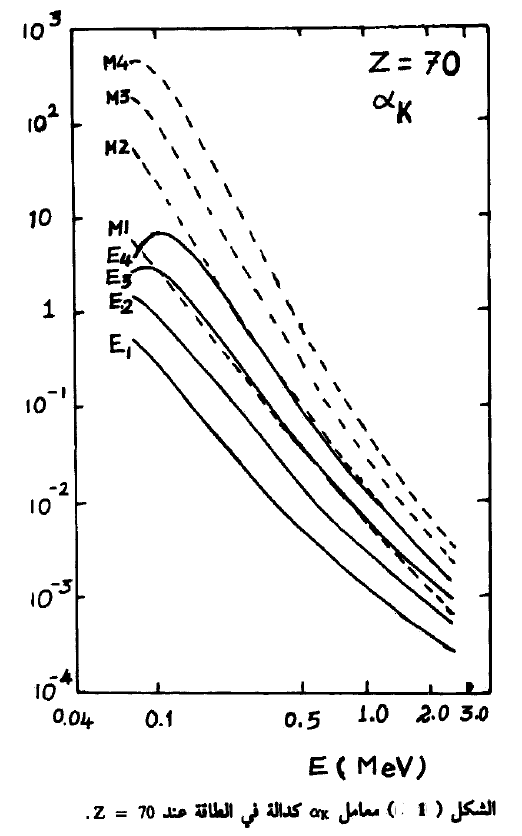
يمكن حساب معاملات التحول (α) نظرياً. حيث أجرى هذه الحسابات سليف وباند Sliv & Band وقاما بجدولة هذه النتائج في جداول خاصة. كما وتوجد أشكال خاصة تعطي هذه القيم لمعظم العناصر. ويبين الشكل (1) معامل aK كدالة في طاقة إثارة المستوى (E) وذلك عند 70= z. حيث يبين الشكل قيم ak عند طاقات مختلفة وقطبية معينة M, E يمكن تعيين _Kα عملياً وبمقارنة هذه النتائج العملية مع الحسابات النظرية فإنه يمكننا تعيين قطبية أشعة γ الناتجة. ومن ثم يمكن تعيين عزم وانعكاسية مستوى الإثارة النووي. وبالتالي تتضح أهمية تعين معاملات التحول وذلك لاستنتاج معلومات مفيدة عن النواة .

كما ويلعب التحول الداخلي دوراً مهماً في تحلل النواة فقد سبق ربينا أن الانتقال ⁺O⁺→O هو انتقال ممنوع عن طريق إشعاع. ومن ثم فإن البديل هنا هو أن تتخلص النواة من طاقتها في هذه الحالة عن طريق تفاعل التحول الداخلي.

وينتج عن التحول الداخلي إثارة للذرة. إذ يترك الإلكترون المنطلق في تفاعل التحول الداخلي فراغاً في المدار ومن ثم يتطوع الكترون من مدار اعلى من الأول لملىء الفراغ وعندما يحدث ذلك تنطلق أشعة X المميزة Characteristic X- rays للمادة. كما ويمكن أو تتخلص الذرة المثارة من طاقتها مباشرة هي الأخرى عن طريق مشابه لما يحدث في النواة وذلك بإعطاء هذه الطاقة مباشرة إلى الإلكترونات الذرية التي تنطلق خارج الذرة والتي تعرف بالكترونات أوجر Auger Effect وهي الكترونات ذات طاقة منخفضة. ومن ثم يتنافس هذا التفاعل مع أشعة - X المميزة. مثلما يتنافس تفاعل التحول الداخلي مع انطلاق أشعة γ من النواة.

كما ويمكن أن يحدث تفاعل آخر عندما تكون طاقة إثارة النواة كبيرة نسبياً. فعندما تبلغ هذه الطاقة 1.02 م. أ. ف أو أكثر فإن تفاعلاً معينياً يحدث وهو ما يسمى يتفاعل إنتاج الأزواج (Production) لمنهم الداخلي حيث ينتج زوج من الإلكترونات e^- , ⁺e الذي ينطلق في المادة. 

مواضيع ذات صلة

أنواع أخرى من المفاعلات

تصاميم مفاعلات متقدمة

انواع المفاعلات النووية

اضطرابات السمت

لماذا طاقات أعلى؟

معجلات الطاقة الفائقة الإرتفاع

التطوير التاريخي للمعجلات

الحقل المغناطيسي وتأثيراته في البلازما والحقول الأخرى

انعطاف صغير عند النجوم

ما الحرارة في الاندماج النووي

التسخين بالحقن بذرات متعادلة

الاندماج النووي في المختبر