

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Descriptive Statistics-Contingency Table
المؤلف:
Larson, R. and Farber, B.
المصدر:
Elementary Statistics: Picturing the World, 6th ed. Indianapolis: Pearson Higher Education, 2014.
الجزء والصفحة:
...
6-2-2021
1326
A contingency table, sometimes called a two-way frequency table, is a tabular mechanism with at least two rows and two columns used in statistics to present categorical data in terms of frequency counts. More precisely, an 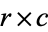 contingency table shows the observed frequency of two variables, the observed frequencies of which are arranged into
contingency table shows the observed frequency of two variables, the observed frequencies of which are arranged into 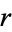 rows and
rows and 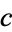 columns. The intersection of a row and a column of a contingency table is called a cell.
columns. The intersection of a row and a column of a contingency table is called a cell.
| gender | cup | cone | sundae | sandwich | other |
| male | 592 | 300 | 204 | 24 | 80 |
| female | 410 | 335 | 180 | 20 | 55 |
For example, the above contingency table has two rows and five columns (not counting header rows/columns) and shows the results of a random sample of 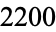 adults classified by two variables, namely gender and favorite way to eat ice cream (Larson and Farber 2014). One benefit of having data presented in a contingency table is that it allows one to more easily perform basic probability calculations, a feat made easier still by augmenting a summary row and column to the table.
adults classified by two variables, namely gender and favorite way to eat ice cream (Larson and Farber 2014). One benefit of having data presented in a contingency table is that it allows one to more easily perform basic probability calculations, a feat made easier still by augmenting a summary row and column to the table.
| gender | cup | cone | sundae | sandwich | other | total |
| male | 592 | 300 | 204 | 24 | 80 | 1200 |
| female | 410 | 335 | 180 | 20 | 55 | 1000 |
| total | 1002 | 635 | 384 | 44 | 135 | 2200 |
The above table is an extended version of the first table obtained by adding a summary row and column. These summaries allow easier computation of several different probability-related quantities. For example, there's a 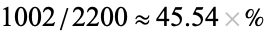 probability that the person sampled prefers their ice cream in a cup, while the probability that a random participant is female is
probability that the person sampled prefers their ice cream in a cup, while the probability that a random participant is female is 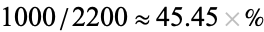 . What's more, computing conditional probabilities is made easier using contingency tables, e.g., the probability that a person prefers ice cream sandwiches given that the person is male is
. What's more, computing conditional probabilities is made easier using contingency tables, e.g., the probability that a person prefers ice cream sandwiches given that the person is male is 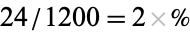 , while the conditional probability that a person is male given that ice cream sandwiches are preferred is
, while the conditional probability that a person is male given that ice cream sandwiches are preferred is 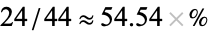 .
.
Other common statistical analyses can be performed on data given in contingency table form. For example, one useful value to know is the so-called expected frequency 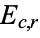 of the cell at the intersection of column
of the cell at the intersection of column 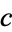 and row
and row 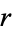 , the formula for which is given by
, the formula for which is given by
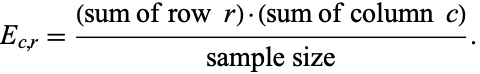 |
(1) |
Computing 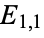 says that the value one would expect at cell
says that the value one would expect at cell 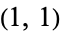 --i.e., the expected number of men who prefer to eat ice cream from a cup--is approximately
--i.e., the expected number of men who prefer to eat ice cream from a cup--is approximately
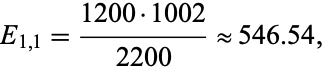 |
(2) |
whereby one may deduce that there are somehow "more than expected" of that particular demographic included in the given sample. Note, too, that knowing 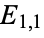 automatically gives, e.g.,
automatically gives, e.g., 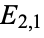 , without repeated application of ():
, without repeated application of ():
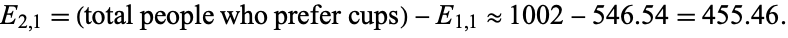 |
(3) |
One of the major benefits of computing expected frequencies is the ability to test whether the two variables being examined--in this case, gender and favorite way to eat ice cream--are actually independent as they've been assumed throughout. This is done by computing, for each cell 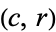 , the expected frequency
, the expected frequency 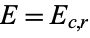 , comparing it to the observed frequency
, comparing it to the observed frequency 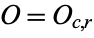 , and then performing a chi-squared test.
, and then performing a chi-squared test.
Another common test associated to contingency tables is so-called homogeneity of proportions test which is a form of chi-squared test used to determine whether several proportions are equal when samples are taken from different populations (Larson and Farber 2014). Worth noting is that both of the above-mentioned instances of chi-squared testing requires a randomly-selected sampling of observed frequencies, each of whose expected frequency is at least 5. These tests play important roles throughout various branches of statistics.
REFERENCES:
Larson, R. and Farber, B. Elementary Statistics: Picturing the World, 6th ed. Indianapolis: Pearson Higher Education, 2014.
Triola, M. F. Elementary Statistics, 11th ed. Boston: Addison-Wesley, 2011.