

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Sociable Numbers
المؤلف:
Cohen, H.
المصدر:
"On Amicable and Sociable Numbers." Math. Comput. 24
الجزء والصفحة:
...
30-11-2020
1122
Sociable numbers are numbers that result in a periodic aliquot sequence, where an aliquot sequence is the sequence of numbers obtained by repeatedly applying the restricted divisor function
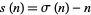 |
(1) |
to 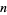 and
and 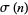 is the usual divisor function.
is the usual divisor function.
If the period of the aliquot cycle is 1, the number is called a perfect number. If the period is 2, the two numbers are called an amicable pair. In general, if the period is 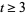 , the number is called sociable of order
, the number is called sociable of order 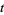 . For example, 1264460 is a sociable number of order four since its aliquot sequence is 1264460, 1547860, 1727636, 1305184, 1264460, ....
. For example, 1264460 is a sociable number of order four since its aliquot sequence is 1264460, 1547860, 1727636, 1305184, 1264460, ....
Only two groups of sociable numbers were known prior to 1970, namely the sets of orders 5 and 28 discovered by Poulet (1918). In 1970, Cohen discovered nine groups of order 4.
The first few sociable numbers are 12496, 14316, 1264460, 2115324, 2784580, 4938136, ... (OEIS A003416), which have orders 5, 28, 4, 4, 4, 4, ... (OEIS A052470). The following table summarizes the smallest members of known social cycles as well as the number of such cycles known (Moews). Excluding perfect numbers, a total of 152 sociable cycles are known as of Feb. 2009 (Pedersen).
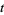 |
OEIS | # | 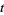 -sociable numbers -sociable numbers |
| 4 | A090615 | 142 | 1264460, 2115324, 2784580, 4938136, 7169104, 18048976, 18656380, ... |
| 5 | 1 | 12496 | |
| 6 | A119478 | 5 | 21548919483, 90632826380, 1771417411016, 3524434872392, 4773123705616 |
| 8 | 2 | 1095447416, 1276254780 | |
| 9 | 1 | 805984760 | |
| 28 | 1 | 14316 |
Y. Kohmoto has considered a generalization of the sociable numbers defined according to the generalized aliquot sequence
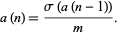 |
(2) |
Multiperfect numbers are fixed points of this mapping, since if 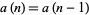 , then
, then
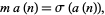 |
(3) |
which is the definition of an 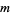 -multiperfect number. If the sequence
-multiperfect number. If the sequence 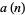 becomes cyclic after
becomes cyclic after 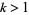 terms, it is then called an
terms, it is then called an  -sociable number of order
-sociable number of order 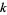 .
.
If 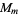 and
and 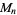 are distinct Mersenne primes, then
are distinct Mersenne primes, then
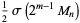 |
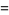 |
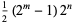 |
(4) |
 |
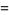 |
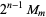 |
(5) |
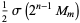 |
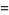 |
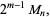 |
(6) |
so 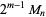 and
and 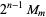 are 1/2-sociable numbers of order 2.
are 1/2-sociable numbers of order 2.
The following table summarizes the smallest members of the generalized 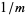 -aliquot sequences of order
-aliquot sequences of order 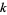 , found by Kohmoto.
, found by Kohmoto.
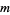 |
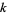 |
starting numbers |
| 3 | 2 | 14913024 |
| 4 | 2 | 2096640, 422688000 |
| 4 | 12 | 3396556800 |
REFERENCES:
Borho, W. "Über die Fixpunkte der 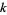 -fach iterierten Teilerersummenfunktion." Mitt. Math. Gesellsch. Hamburg 9, 34-48, 1969.
-fach iterierten Teilerersummenfunktion." Mitt. Math. Gesellsch. Hamburg 9, 34-48, 1969.
Cohen, H. "On Amicable and Sociable Numbers." Math. Comput. 24, 423-429, 1970.
Cohen, G. L. and te Riele, H. J. J. "Iterating the Sum-of-Divisors Function." Amsterdam, Netherlands: Centrum voor Wiskunde en Informatica Report NM-R9525 1995.
Creyaufmüller, W. "Aliquot Sequences." https://www.aliquot.de/aliquote.htm.
Devitt, J. S.; Guy, R. K.; and Selfridge, J. L. Third Report on Aliquot Sequences, Congr. Numer. XVIII, Proc. 6th Manitoba Conf. Numerical Math, pp. 177-204, 1976.
Erdős, P.; Granville, A.; Pomerance, C.; and Spiro, C. "On the Normal Behavior of Iterates of Some Arithmetical Functions." Analytic Number Theory, Proc. Conf. in Honor of P. T. Bateman, Allerton Park, 1989. Boston: Birkhäuser, pp. 165-204, 1990.
Flammenkamp, A. "New Sociable Numbers." Math. Comput. 56, 871-873, 1991.
Gardner, M. "Perfect, Amicable, Sociable." Ch. 12 in Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 160-171, 1978.
Guy, R. K. "Aliquot Cycles or Sociable Numbers." §B7 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 62-63, 1994.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 145-146, 1979.
Moews, D. "A List of Aliquot Cycles of Length Greater than 2." Rev. Jul. 20, 2005. https://djm.cc/sociable.txt.
Moews, D. "Sociable Numbers." https://djm.cc/amicable.html#sociable.
Moews, D. and Moews, P. C. "A Search for Aliquot Cycles Below 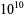 ." Math. Comput. 57, 849-855, 1991.
." Math. Comput. 57, 849-855, 1991.
Moews, D. and Moews, P. C. "A Search for Aliquot Cycles and Amicable Pairs." Math. Comput. 61, 935-938, 1993.
Pedersen, J. A. M. "Tables of Aliquot Cycles." https://amicable.homepage.dk/tables.htm.
Poulet, P. Question 4865. L'interméd. des Math. 25, 100-101, 1918.
Root, S. Item 61 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 23, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item61.
Sloane, N. J. A. Sequences A003416, A052470, A090615, and A119478 in "The On-Line Encyclopedia of Integer Sequences."
te Riele, H. J. J. "Perfect Numbers and Aliquot Sequences." In Computational Methods in Number Theory, Part I. (Ed. H. W. Lenstra Jr. and R. Tijdeman). Amsterdam, Netherlands: Mathematisch Centrum, pp. 141-157, 1982.