Bertrand's postulate, also called the Bertrand-Chebyshev theorem or Chebyshev's theorem, states that if 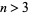, there is always at least one prime  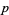between  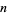and 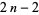. Equivalently, if 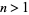, then there is always at least one prime  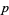such that 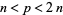. The conjecture was first made by Bertrand in 1845 (Bertrand 1845; Nagell 1951, p. 67; Havil 2003, p. 25). It was proved in 1850 by Chebyshev (Chebyshev 1854; Havil 2003, p. 25; Derbyshire 2004, p. 124) using non-elementary methods, and is therefore sometimes known as Chebyshev's theorem. The first elementary proof was by Ramanujan, and later improved by a 19-year-old Erdős in 1932.

A short verse about Bertrand's postulate states, "Chebyshev said it, but I'll say it again; There's always a prime between 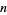 and 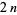." While commonly attributed to Erdős or to some other Hungarian mathematician upon Erdős's youthful re-proof the theorem (Hoffman 1998), the quote is actually due to N. J. Fine (Schechter 1998).

An extension of this result is that if 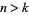, then there is a number containing a prime divisor  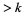in the sequence 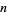, , 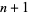..., 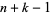. (The case  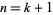then corresponds to Bertrand's postulate.) This was first proved by Sylvester, independently by Schur, and a simple proof was given by Erdős (1934; Hoffman 1998, p. 37)

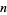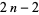The numbers of primes between  and  for 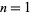, 2, ... are 0, 0, 0, 1, 1, 1, 1, 2, 2, 3, 3, 3, 3, 3, 3, 4, ... (OEIS A077463), while the numbers of primes between  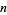and 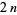 are 0, 1, 1, 2, 1, 2, 2, 2, 3, 4, 3, 4, 3, 3, ... (OEIS A060715). For 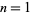, 2, ..., the values of 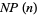, where  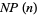is the next prime function are 2, 3, 5, 5, 7, 7, 11, 11, 11, 11, 13, 13, 17, 17, 17, 17, 19, ... (OEIS A007918).

After his proof of Bertrand's postulate, Ramanujan (1919) proved the generalization that 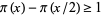, 2, 3, 4, 5, ... if 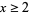, 11, 17, 29, 41, ... (OEIS A104272), respectively, where  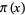is the prime counting function. The numbers are sometimes known as Ramanujan primes. The case  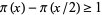for all  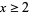is Bertrand's postulate.

A related problem is to find the least value of 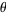 so that there exists at least one prime between  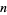and 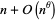 for sufficiently large  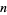(Berndt 1994). The smallest known value is  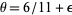(Lou and Yao 1992).

REFERENCES:

Aigner, M. and Ziegler, G. M. Proofs from the Book, 2nd ed. New York: Springer-Verlag, 2000.

Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, p. 135, 1994.

Bertrand, J. "Mémoire sur le nombre de valeurs que peut prendre une fonction quand on y permute les lettres qu'elle renferme." J. l'École Roy. Polytech. 17, 123-140, 1845.

Chebyshev, P. "Mémoire sur les nombres premiers." Mém. Acad. Sci. St. Pétersbourg 7, 17-33, (1850) 1854. Reprinted as §1-7 in Œuvres de P. L. Tschebychef, Tome I. St. Pétersbourg, Russia: Commissionaires de l'Academie Impériale des Sciences, pp. 51-64, 1899.

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.

Dickson, L. E. "Bertrand's Postulate." History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 435-436, 2005.

Erdős, P. "Ramanujan and I." In Proceedings of the International Ramanujan Centenary Conference held at Anna University, Madras, Dec. 21, 1987. (Ed. K. Alladi). New York: Springer-Verlag, pp. 1-20, 1989.

Erdős, P. "A Theorem of Sylvester and Schur." J. London Math. Soc. 9, 282-288, 1934.

Hardy, G. H. and Wright, E. M. "Bertrand's Postulate and a 'Formula' for Primes." §22.3 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 343-345 and 373, 1979.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, 1998.

Lou, S. and Yau, Q. "A Chebyshev's Type of Prime Number Theorem in a Short Interval (II)." Hardy-Ramanujan J. 15, 1-33, 1992.

Nagell, T. Introduction to Number Theory. New York: Wiley, p. 70, 1951.

Ramanujan, S. "A Proof of Bertrand's Postulate." J. Indian Math. Soc. 11, 181-182, 1919.

Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., pp. 208-209, 2000.

Schechter, B. My Brain is Open: The Mathematical Journeys of Paul Erdős. New York: Simon and Schuster, 1998.

Séroul, R. Programming for Mathematicians. Berlin: Springer-Verlag, pp. 7-8, 2000.

Sloane, N. J. A. Sequences A007918, A060715, A077463, and A104272 in "The On-Line Encyclopedia of Integer Sequences."