

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Plastic Constant
المؤلف:
Finch, S. R
المصدر:
Mathematical Constants. Cambridge, England: Cambridge University Press
الجزء والصفحة:
...
20-1-2020
1048
The plastic constant 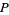 , sometimes also called the silver number or plastic number, is the limiting ratio of the successive terms of the Padovan sequence and Perrin sequence. It is given by
, sometimes also called the silver number or plastic number, is the limiting ratio of the successive terms of the Padovan sequence and Perrin sequence. It is given by
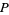 |
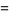 |
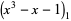 |
(1) |
 |
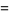 |
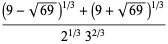 |
(2) |
 |
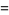 |
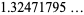 |
(3) |
(OEIS A060006), where 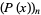 denotes a polynomial root. It is therefore an algebraic number of degree 3.
denotes a polynomial root. It is therefore an algebraic number of degree 3.
It is also given by
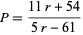 |
(4) |
where
![r=-1/5[-j(tau_0)]^(1/3),](http://mathworld.wolfram.com/images/equations/PlasticConstant/NumberedEquation2.gif) |
(5) |
where 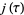 is the
is the 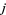 -function and the half-period ratio is equal to
-function and the half-period ratio is equal to 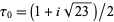 .
.
The plastic constant 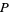 was originally studied in 1924 by Gérard Cordonnier when he was 17. In his later correspondence with Dom Hans van der Laan, he described applications to architecture, using the name "radiant number." In 1958, Cordonnier gave a lecture tour that illustrated the use of the constant in many existing buildings and monuments (C. Mannu, pers comm., Mar. 11, 2006).
was originally studied in 1924 by Gérard Cordonnier when he was 17. In his later correspondence with Dom Hans van der Laan, he described applications to architecture, using the name "radiant number." In 1958, Cordonnier gave a lecture tour that illustrated the use of the constant in many existing buildings and monuments (C. Mannu, pers comm., Mar. 11, 2006).
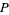 satisfies the algebraic identities
satisfies the algebraic identities
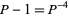 |
(6) |
and
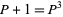 |
(7) |
and is therefore is one of the numbers  for which there exist natural numbers
for which there exist natural numbers 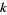 and
and 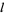 such that
such that 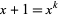 and
and 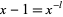 . It was proven by Aarts et al. (2001) that
. It was proven by Aarts et al. (2001) that 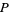 and the golden ratio
and the golden ratio 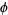 are in fact the only such numbers.
are in fact the only such numbers.
The identity 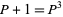 leads to the beautiful nested radical identity
leads to the beautiful nested radical identity
|
(8) |
The plastic constant is also connected with the ring of integers 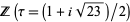 of the number field
of the number field 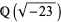 since it the real root of the Weber function for the smallest negative discriminant with class number 3, namely
since it the real root of the Weber function for the smallest negative discriminant with class number 3, namely 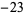 . In particular,
. In particular,
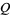 |
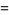 |
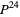 |
(9) |
 |
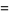 |
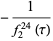 |
(10) |
 |
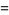 |
![-[(eta(tau))/(sqrt(2)eta(2tau))]^(24)](http://mathworld.wolfram.com/images/equations/PlasticConstant/Inline36.gif) |
(11) |
 |
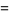 |
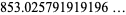 |
(12) |
(OEIS A116397), where 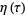 is the Dedekind eta function.
is the Dedekind eta function.
The plastic constant is also the smallest Pisot number.
The plastic constant satisfies the near-identity
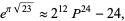 |
(13) |
where the difference is 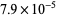 .
.
Surprisingly, the plastic constant is connected to the metric properties of the snub icosidodecadodecahedron.
REFERENCES:
Aarts, J.; Fokkink, R. J.; and Kruijtzer, G. "Morphic Numbers." Nieuw Arch. Wisk 5-2, 56-58, 2001. http://www.math.leidenuniv.nl/~naw/serie5/deel02/mrt2001/pdf/archi.pdf.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, p. 9, 2003.
Gazale, M. J. Ch. 7 in Gnomon: From Pharaohs to Fractals. Princeton, NJ: Princeton University Press, 1999.
Piezas, T. "Ramanujan's Constant and Its Cousins." http://www.geocities.com/titus_piezas/Ramanujan_a.htm.
Sloane, N. J. A. Sequences A060006 and A116397 in "The On-Line Encyclopedia of Integer Sequences."
Stewart, I. "Tales of a Neglected Number." Sci. Amer. 274, 102-103, Jun. 1996.
van der Laan, H. Le Nombre Plastique: quinze Leçons sur l'Ordonnance architectonique. Leiden: Brill, 1960.
Weng, A. "Class Polynomials of CM-Fields." http://www.exp-math.uni-essen.de/zahlentheorie/classpol/class.html.