Laplace Equation--Confocal Ellipsoidal Coordinates
المؤلف:
Morse, P. M. and Feshbach, H
المصدر:
Methods of Theoretical Physics, Part I. New York: McGraw-Hill
الجزء والصفحة:
...
21-7-2018
2632
Laplace Equation--Confocal Ellipsoidal Coordinates
Using the notation of Byerly (1959, pp. 252-253), Laplace's equation can be reduced to
 |
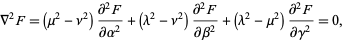(1)
|
where
In terms of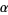 
, 
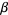, and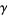 
,
Equation (◇) is not separable using a function of the form
 |
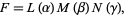(11)
|
but it is if we let
These give
and all others terms vanish. Therefore (◇) can be broken up into the equations
For future convenience, now write
then
Now replace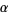 
, 
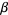, and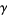 
to obtain
![(lambda^2-b^2)(lambda^2-c^2)(d^2L)/(dlambda^2)+lambda(lambda^2-b^2+lambda^2-c^2)(dL)/(dlambda)
-[m(m+1)lambda^2-(b^2+c^2)p]L=0
(mu^2-b^2)(mu^2-c^2)(d^2M)/(dmu^2)+mu(mu^2-b^2+mu^2-c^2)(dM)/(dmu)
-[m(m+1)mu^2-(b^2+c^2)p]M=0
(nu^2-b^2)(nu^2-c^2)(d^2N)/(dnu^2)+nu(nu^2-b^2+nu^2-c^2)(dN)/(dnu)
-[m(m+1)nu^2-(b^2+c^2)p]N=0.](http://mathworld.wolfram.com/images/equations/LaplaceEquationConfocalEllipsoidalCoordinates/NumberedEquation3.gif) |
(25)
|
Each of these is a Lamé's differential equation, whose solution is called an ellipsoidal harmonic of the first kind. Writing
gives the solution to (◇) as a product of ellipsoidal harmonics of the first kind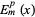 
.
 |
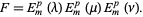(29)
|
REFERENCES:
Arfken, G. "Confocal Ellipsoidal Coordinates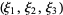 
." §2.15 in Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 117-118, 1970.
Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, pp. 251-258, 1959.
Moon, P. and Spencer, D. E. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, pp. 43-44, 1988.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 663, 1953.
الاكثر قراءة في المعادلات التفاضلية الجزئية
اخر الاخبار
اخبار العتبة العباسية المقدسة
