The matrix formulation of the Hückel method
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص388-390
2025-11-29
34
The matrix formulation of the Hückel method
In preparation for making Hückel theory more sophisticated and readily applicable to bigger molecules, we need to reformulate it in terms of matrices and vectors (see Appendix 2). We have seen that the secular equations that we have to solve for a two-atom system have the form
(HAA −EiSAA) c i, A+ (HAB − EiSAB) ci, B= 0
(HBA−EiSBA) c i, A+ (HBB − EiSBB) ci, B= 0
where the eigenvalue Ei corresponds to a wavefunction of the form ψ i = c i, AA + c i, BB. (These expressions generalize eqn 11.25). There are two atomic orbitals, two eigen values, and two wavefunctions, so there are two pairs of secular equations, with the first corresponding to E1 and ψ1:
(HAA −E1SAA) c 1,A + (HAB − E1SBA)c1,B = 0
(HBA −E1SBA) c 1,A + (HBB − E1SBB)c1,B = 0
and another corresponding to E2 and ψ2:
(HAA −E2SAA) c 2,A + (HAB − E2SAB)c2,B = 0
(HBA −E2SBA) c 2,A + (HBB − E2SBB)c2,B = 0
If we introduce the following matrices and column vectors
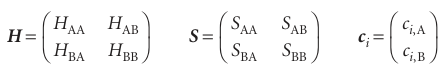
then each pair of equations may be written more succinctly as
(H−EiS) ci = 0 or Hci=SciEi
where H is the hamiltonian matrix and S is the overlap matrix. To proceed with the calculation of the eigenvalues and coefficients, we introduce the matrices
for then the entire set of equations we have to solve can be expressed as
HC=SCE
In the Hückel approximation, HAA=HBB=α,HAB=HBA=β, and we neglect overlap, setting S=1, the unit matrix (with 1 on the diagonal and 0 elsewhere). Then
HC=CE
At this point, we multiply from the left by the inverse matrix C−1, and find
C−1HC=E
where we have used C−1C=1. In other words, to find the eigenvalues Ei, we have to find a transformation of H that makes it diagonal. This procedure is called matrix diagonalization. The diagonal elements then correspond to the eigenvalues Ei and the columns of the matrix Cthat brings about this diagonalization are the coefficients of the members of the basis set, the set of atomic orbitals used in the calculation, and hence give us the composition of the molecular orbitals. If there are Norbitals in the basis set (there are only two in our example), then there are Neigenvalues Ei and N corresponding column vectors ci. As a result, we have to solve Nequations of the form Hci=SciEi by diagonalization of the N×N matrix H, as directed by eqn 11.46.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
