Ethene and frontier orbitals
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص387-388
2025-11-29
30
Ethene and frontier orbitals
We express the π orbitals as LCAOs of the C2p orbitals that lie perpendicular to the molecular plane. In ethene, for instance, we would write , ψ=cAA+cBB , where the A is a C2p orbital on atom A, and so on. Next, the optimum coefficients and energies are found by the variation principle as explained in Section 11.5. That is, we have to solve the secular determinant, which in the case of ethene is eqn 11.29 with αA=αB=α:
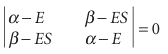
The roots of this determinant can be found very easily (they are the same as those in Illustration 11.2). In a modern computation all the resonance integrals and overlap integrals would be included, but an indication of the molecular orbital energy level diagram can be obtained very readily if we make the following additional Hückel approximations:
1 All overlap integrals are set equal to zero.
2 All resonance integrals between non-neighbours are set equal to zero.
3 All remaining resonance integrals are set equal (to β). These approximations are obviously very severe, but they let us calculate at least a general picture of the molecular orbital energy levels with very little work. The assumptions result in the following structure of the secular determinant:
1 All diagonal elements: α − E.
2 Off-diagonal elements between neighbouring atoms: β.
3 All other elements: 0.
These approximations lead to
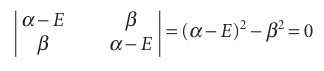
The roots of the equation are , E± =α±β , The + sign corresponds to the bonding combination (β is negative) and the − sign corresponds to the antibonding combination (Fig. 11.38). We see the effect of neglecting overlap by comparing this result with eqn 11.31. The building-up principle leads to the configuration 1π2, because each carbon atom supplies one electron to the π system. The highest occupied molecular orbital in ethene, its HOMO, is the 1π orbital; the lowest unfilled molecular orbital, its LUMO, is the 2π orbital (or, as it is sometimes denoted, the 2π* orbital). These two orbitals jointly form the frontier orbitals of the molecule. The frontier orbitals are important because they are largely responsible for many of the chemical and spectroscopic properties of the molecule. For example, we can estimate that 2|β| is the π* ← π excitation energy of ethene, the energy required to excite an electron from the 1π to the 2π orbital. The constant βis often left as an adjustable parameter; an approximate value for πbonds formed from overlap of two C2p atomic orbitals is about −2.4 eV (−230 kJ mol−1).
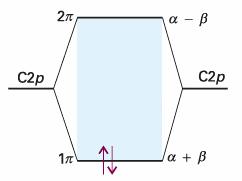
Fig. 11.38 The Hückel molecular orbital energy levels of ethene. Two electrons occupy the lower π orbital.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
